Equilateral in an Ellipse
An equilateral triangle △ A B C is inscribed in a horizontal ellipse so that it has vertical symmetry and so that two of its sides pass through the ellipse's focal points F 1 and F 2 , as shown below. If the distance between the focal points is 5 , find the perimeter of the equilateral triangle.
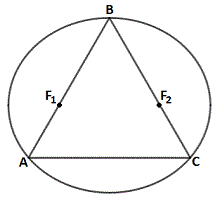
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the semi-major axis of the ellipse be a , the semi-minor axis be b and the eccentricity be e . Then 2 a e = 5 ⟹ a e = 2 5 .
tan 6 0 ° = 3 = a e b = 2 5 b ⟹
b = 2 5 3 ⟹ a = 5 ⟹ the equation of the ellipse is 3 x 2 + 4 y 2 = 7 5 .
If the position coordinates of one end of the base of the triangle be ( p , q ) , then
3 p 2 + 4 × 3 ( p + 2 5 ) 2 = 7 5 ⟹
p = 0 , q = 2 5 3 and p = − 4 , q = − 2 3 3 .
Hence, length of each side of the triangle is
1 6 + ( 2 − 3 3 − 2 5 3 ) 2 = 8 ,
and the perimeter is 3 × 8 = 2 4 .
Choose a coordinate system so that the ellipse has an equation of the form (x/a)^2 + (y/b)^2 = 1. Then, since the foci are 5 units apart, their coordinates are at (2.5, 0) and (-2.5, 0). Therefore, trigonometry yields b = 2.5 tan(60 degrees) = 2.5 sqrt(3). From this, the coordinates of B are (0, 2.5 sqrt(3)). The slope of the line containing BC is thus = (2.5 sqrt(3) - 0)/(0-(2.5)) = -sqrt(3). Then, the equation of the line containing segment BC is y = -sqrt(3) (x-2.5). Utilizing the equation for the foci of an ellipse allows us to discover that a = 5, so that the ellipse has equation (x/5)^2 + (y/(2.5 sqrt(3))^2 = 1. Substituting the equation of this line into the equation of the ellipse and simplifying shows that the coordinates of point C are (4, -1.5 sqrt(3)). By symmetry, the coordinates of A are (-4, -1.5 sqrt(3)). Therefore, the distance between A and C is 8 units, and the perimeter is 8*3 = 24 units.
Let x = A B = A C = B C , and draw F 1 F 2 and F 1 C .
By symmetry, △ B F 1 F 2 is also an equilateral triangle, so ∠ B F 1 F 2 = ∠ F 1 F 2 B = F 1 B F 2 = 6 0 ° , and since the distance between focal points is 5 , F 1 F 2 = B F 1 = B F 2 = 5 .
Since B C = x and B F 2 = 5 , C F 2 = x − 5 .
Since the sum of the distances between a point on an ellipse and the two focal points is a constant, B F 1 + B F 2 = C F 1 + C F 2 , or 5 + 5 = C F 1 + x − 5 , which means C F 1 = 1 5 − x .
By the law of cosines on △ B C F 1 , ( 1 5 − x ) 2 = x 2 + 5 2 − 2 ⋅ x ⋅ 5 ⋅ cos 6 0 ° , which solves to x = 8 , so that the perimeter is P = 3 x = 3 ⋅ 8 = 2 4 .