Equilateral nine-side-polygon
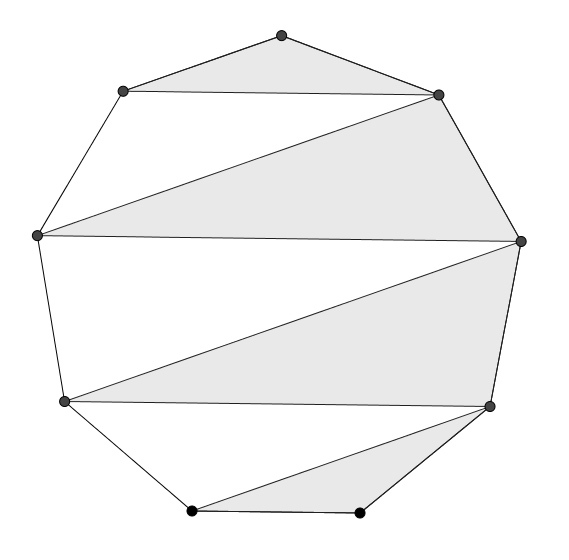
Consider the above regular 9-gon.
Which area is larger: the black or the white are?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
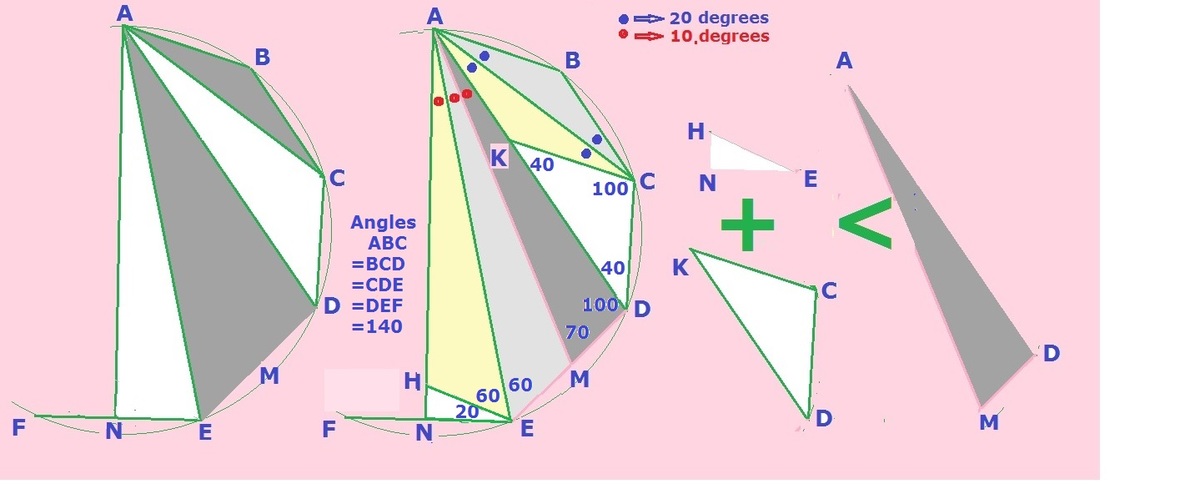
Let AN be the altitude of isosceles triangle AFE in 9-gon ABCDEF.....So AN is the line of symmetry.
So consider only half 9-gon.
WLOG let the sides of the 9-gon be unit. So AB=BC=CD=DE=EF=1, EN=1/2.
Let AM be the angle bisector of DAE, M on DE.
Construct AKC congruent to ABC, .....AHE congruent to AME.
So net white area not canceled is EHN +CKD, net black area not canceled is AMD.
S u m o f a n g l e s o f a t r i a n g l e i s 1 8 0 . E x t e r n a l a n g l e o f a t r i a n g l e i s e q u a l t o t h e s u m o f i n t e r n a l a n g l e s . ∴ w e g e t t h e a n g l e s s h o w n i n t h e f i g . A r e a o f r t . ∠ Δ E H N = 1 / 2 ∗ 1 / 2 ∗ 1 / 2 / t a n 7 0 = . 0 4 5 5 . I n i s o s c e l e s Δ C K D , v e r t e x ∠ D C K = 1 0 0 , a n d e q u a l s i d e s = 1 . ∴ a r e a C K D = 1 / 2 ∗ 1 ∗ 1 ∗ s i n 1 0 0 = 0 . 4 9 2 4 . I n A M D , u s i n g S i n L a w , A D / s i n 7 0 = M D / s i n 1 0 . A r e a A M D = 1 / 2 ∗ A D ∗ A M ∗ s i n D A M . A D = A K + K D = 1 + 2 ∗ c o s 4 0 . A r e a A M D = 1 / 2 ∗ ( 1 + 2 ∗ c o s 4 0 ) 2 ∗ s i n 1 0 / s i n 7 0 ∗ s i n 1 0 0 = . 5 8 3 4 . ∴ B l a c k a r e a = 2 ∗ . 5 8 3 4 > w h i t e a r e a = 2 ∗ ( 0 . 4 9 2 4 + . 0 4 5 5 ) .
If we filled two triangles with same way, then their areas are equal.