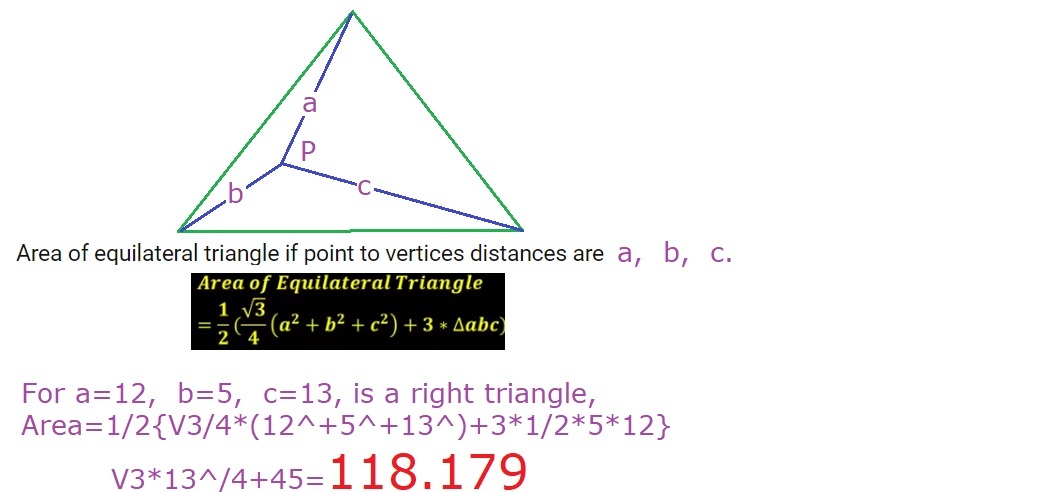
Equilateral triangle point
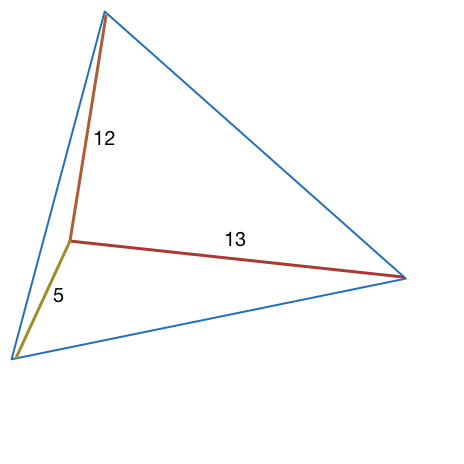 Let
A
B
C
an equilateral triangle,
P
a point inside the triangle such as
A
P
=
5
,
B
P
=
1
2
and
C
P
=
1
3
. Find the area of
△
A
B
C
.
Let
A
B
C
an equilateral triangle,
P
a point inside the triangle such as
A
P
=
5
,
B
P
=
1
2
and
C
P
=
1
3
. Find the area of
△
A
B
C
.
The answer is 118.179.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
http://mathforum.org/library/drmath/view/61863.html
Why is triangle P'PB aright triangle?
Log in to reply
I also ask
5 2 + 1 2 2 = 1 3 2 so 5, 12, 13 is a Pythagorean triple. Or, using the law of cosine again: 1 3 2 = 5 2 + 1 2 2 − 2 × 5 × 1 2 × cos ( α ) leading to c o s ( α ) = 0 or α = 9 0 °
rotational geometry
Did the same. 2 minutes of silence for those trying to solve this using heron's formula and algebra! :D
Log in to reply
Yeah, I did it like that. I was systematic and methodical to set up the equations. It took about 15 minutes to do this properly. Then I plugged them into Wolfram Alpha to get a solution for the length of each side of the triangle and the overall area.
Hahaha :')
How is triangle AP'P equilateral ? I can't see clearly :-P
Indeed, a great solution with a very unique and creative solution. Keep up the creativity.
△ A P C is rotated over 6 0 ° .
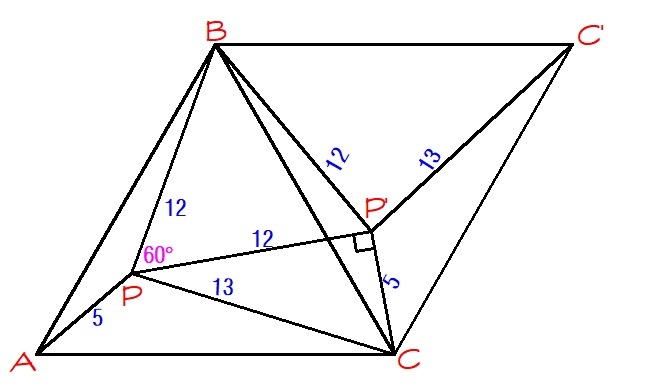 Rotate
△
A
B
C
with a magnitude of
6
0
∘
in a counter-clockwise direction making point
B
as the pivot point.
△
B
P
P
′
is an equilateral
△
and
△
5
−
1
2
−
1
3
is a right triangle. Then,
cos
∠
P
′
P
C
=
1
2
5
, such that
∠
P
′
P
C
≈
2
2
.
6
2
. By cosine law (or cosine rule or law of cosines) on
△
B
P
C
, we have
(
B
C
)
2
=
1
2
2
+
1
3
2
−
2
(
1
2
)
(
1
3
)
[
cos
(
2
2
.
6
2
+
6
0
)
]
≈
2
7
2
.
9
2
4
. Since
△
A
B
C
is equilateral, the area is
2
1
(
B
C
)
2
(
sin
6
0
)
=
2
1
(
2
7
2
.
9
2
4
)
(
sin
6
0
)
≈
1
1
8
.
1
7
9
Rotate
△
A
B
C
with a magnitude of
6
0
∘
in a counter-clockwise direction making point
B
as the pivot point.
△
B
P
P
′
is an equilateral
△
and
△
5
−
1
2
−
1
3
is a right triangle. Then,
cos
∠
P
′
P
C
=
1
2
5
, such that
∠
P
′
P
C
≈
2
2
.
6
2
. By cosine law (or cosine rule or law of cosines) on
△
B
P
C
, we have
(
B
C
)
2
=
1
2
2
+
1
3
2
−
2
(
1
2
)
(
1
3
)
[
cos
(
2
2
.
6
2
+
6
0
)
]
≈
2
7
2
.
9
2
4
. Since
△
A
B
C
is equilateral, the area is
2
1
(
B
C
)
2
(
sin
6
0
)
=
2
1
(
2
7
2
.
9
2
4
)
(
sin
6
0
)
≈
1
1
8
.
1
7
9
Note:
I used the formula A = 2 1 a b sin C for the area of the triangle.
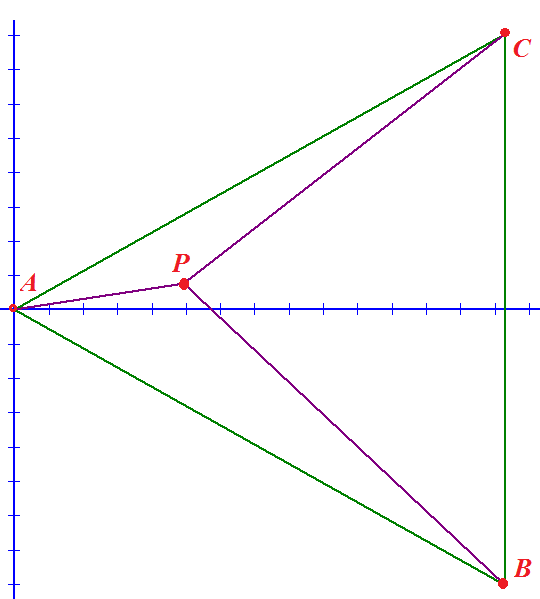
I solved this by using analytic geometry.
Let s be the side length of △ A B C . Place the triangle on a Cartesian coordinate system such that A = ( 0 , 0 ) , B = ( 2 3 s , − 2 s ) , C = ( 2 3 s , 2 s ) and P = ( a , b ) . Using the lengths of P A , P B , P C and the formula for the distance between 2 points, we get the following system of equations:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ( 1 ) : ( 2 ) : ( 3 ) : a 2 + b 2 = 5 2 = 2 5 ( 2 3 s − a ) 2 + ( b + 2 s ) 2 = 1 3 2 = 1 6 9 ( 2 3 s − a ) 2 + ( b − 2 s ) 2 = 1 2 2 = 1 4 4
Subtracting ( 3 ) from ( 2 ) gives us 2 b s = 2 5 . ( 4 )
Now using ( 1 ) and ( 4 ) we get a 2 s 2 + b 2 s 2 = 2 5 s 2 → a 2 s 2 = 2 5 s 2 − 4 6 2 5 . ( 5 )
Next let's expand equation ( 2 ) : 4 3 s 2 − 3 s a + a 2 + b 2 + b s + 4 s 2 = 1 6 9 Simplify using ( 1 ) and ( 4 ) : s 2 − 2 2 6 3 = 3 s a Now square the equation and rewrite using ( 5 ) : s 4 − 2 6 3 s 2 + 4 6 9 1 6 9 = 3 a 2 s 2 = 7 5 s 2 − 4 1 8 7 5 s 4 − 3 3 8 s 2 + 1 7 7 6 1 = 0 ( s 2 − 1 6 9 ) 2 = 1 0 8 0 0 s 2 = 1 6 9 ± 6 0 3
Hence the area of the triangle is 4 3 s 2 = 4 1 6 9 3 ± 4 5 .
The minus option would create a triangle that is too small to fit point P inside it. Therefore the area is 4 1 6 9 3 + 4 5 ≈ 1 1 8 . 7 9
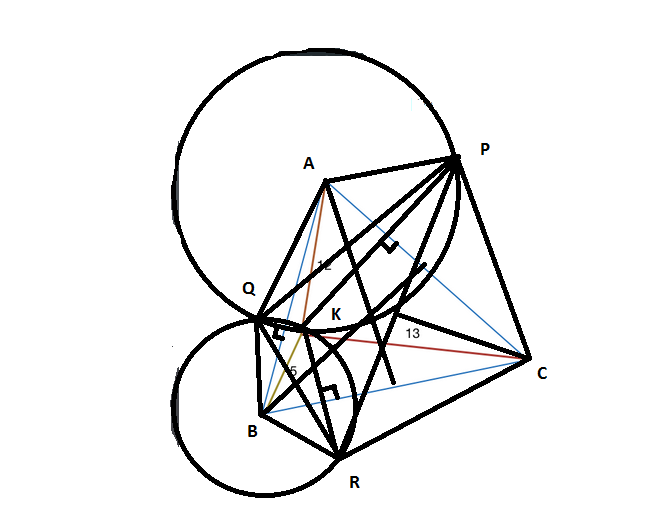 It is easy to realize that three triangles PCR, PAQ, BQR are isosceles triangle with three angles are 30, 30, 60 degrees.
So applying heron theory to get:
S
(
A
B
C
)
=
(
2
3
)
4
×
(
1
3
+
5
−
1
2
)
×
(
1
3
−
5
+
1
2
)
×
(
1
3
+
5
+
1
2
)
×
(
1
3
+
5
+
1
2
)
+
2
1
×
2
3
×
(
1
3
2
+
5
2
+
1
2
2
)
=
1
1
8
.
1
7
9
It is easy to realize that three triangles PCR, PAQ, BQR are isosceles triangle with three angles are 30, 30, 60 degrees.
So applying heron theory to get:
S
(
A
B
C
)
=
(
2
3
)
4
×
(
1
3
+
5
−
1
2
)
×
(
1
3
−
5
+
1
2
)
×
(
1
3
+
5
+
1
2
)
×
(
1
3
+
5
+
1
2
)
+
2
1
×
2
3
×
(
1
3
2
+
5
2
+
1
2
2
)
=
1
1
8
.
1
7
9
So messy but nice
rối quá anh @.@
Rotate APB about A until AB coincide with AC. Let the new location of P be denoted by Q. So triangle APQ is equilateral. Moreover, PQC is a 5-12-13 right triangle. Therefore AQC = AQP+PQC = 60+90 = 150. By law of cosines,
AC^2
= AQ^2+QC^2-2 AQ QC*cos(AQC)
= 25+144-60*sqrt(3)
= 169+60*sqrt(3).
It follows that the area of triangle ABC is AC^2 sqrt(3)/4 = 45+169 sqrt(3)/4 ~ 118.18.
We first rotate △ A P C so that C goes to B . Name the image of point Q . Rotate triangles C P B and B P A in a similar fashion, naming the images of point P R and S respectively. Notice that the area of hexagon A S C Q B R is twice the area of triangle A B C because each of the triangles A P C , C P B , and B P A occur twice in A S C Q B R . So we will calculate the area of the hexagon and divide by 2 . Draw the lines P Q , P R , and P S and observe the resulting triangles. The angles P C Q , P B R , and P A S are 6 0 degrees because triangle A B C is equilateral and our construction preserves angles. Therefore triangles Q P C , R P B , and P S A are equilateral with side lengths 13,12,5 respectively. These will have total area 4 5 2 3 + 4 1 2 2 3 + 4 1 3 2 3 = 2 1 6 9 3 The remaining triangles are 5-12-13 triangles, so they will have total area 2 1 ⋅ 5 ⋅ 1 2 + 2 1 ⋅ 5 ⋅ 1 2 + 2 1 ⋅ 5 ⋅ 1 2 = 9 0 So the total area of the hexagon is [ A S C Q B R ] = 9 0 + 2 1 6 9 3 Which means [ A B C ] = 2 1 [ A S C Q B R ] = 4 5 + 4 1 6 9 3 ≈ 1 1 8 . 1 8
a b c De, Prithwijit, "Curious properties of the circumcircle and incircle of an equilateral triangle," Mathematical Spectrum 41(1), 2008-2009, 32-35. (For any point P in the plane, with distances p, q, and t from the vertices A, B, and C respectively,[17]) http://en.wikipedia.org/wiki/Equilateral triangle#cite note-De-17
My solution's a bit more rigorous (basically, it involves solving a 3 x 3 system of the Law of Cosines). Let angle ∠ A P B = x , ∠ B P C = y , ∠ A P C = 3 6 0 − x − y degrees. Let the side of the equilateral △ A B C equal s . One now now obtains the system:
s 2 = 5 2 + 1 2 2 − 2 ( 5 ) ( 1 2 ) ⋅ cos ( x ) ,
s 2 = 1 2 2 + 1 3 2 − 2 ( 1 2 ) ( 1 3 ) ⋅ cos ( y ) ,
s 2 = 5 2 + 1 3 2 − 2 ( 5 ) ( 1 3 ) ⋅ cos ( 3 6 0 − x − y ) .
I solved the system for x = 1 5 0 degrees, which gives the area of △ A B C as 4 3 ⋅ s 2 = 4 3 ⋅ [ 5 2 + 1 2 2 − 1 2 0 ∗ ( − 2 3 ) ] = 1 6 9 ⋅ 4 3 + 4 5 = 1 1 8 . 1 8 square units.
I tried something similar , but then one has to relate cos(A+B+C) when A + B + C = 2*pi to cos(A) + cos(B) + cos(C). (Of course , one could express everything in terms of cos(A) )
Reason for taking x=150 ?
My solution was this.
First moves △ A P C together △ A P B as image shows, clearly, △ A P ′ P is an equilateral triangle and △ P P ′ B is an rectangle triangle so ∠ B P A = 6 0 ° + 9 0 ° = 1 5 0 ° .
By law of cosines, A B 2 = 5 2 + 1 2 2 − 2 × 5 × 1 2 × c o s 1 5 0 ° = 1 6 9 + 6 0 3 .
Therefore △ A B C is
4 3 × ( 1 6 9 + 6 0 3 ) = 4 5 + 4 1 6 9 3 ≈ 1 1 8 . 1 7 9