Equilateral Sangaku
In an equilateral triangle ABC of side 8 units lines BEF, CFD, ADE are drawn making equal angles with AB, BC, CA, respectively, forming the triangle DEF, and so that the radius 'r' of the in-circle of triangle DEF is equal to the radii of the incircles of triangles ABE, BCF, and ACD.
Determine the value of 'r'.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
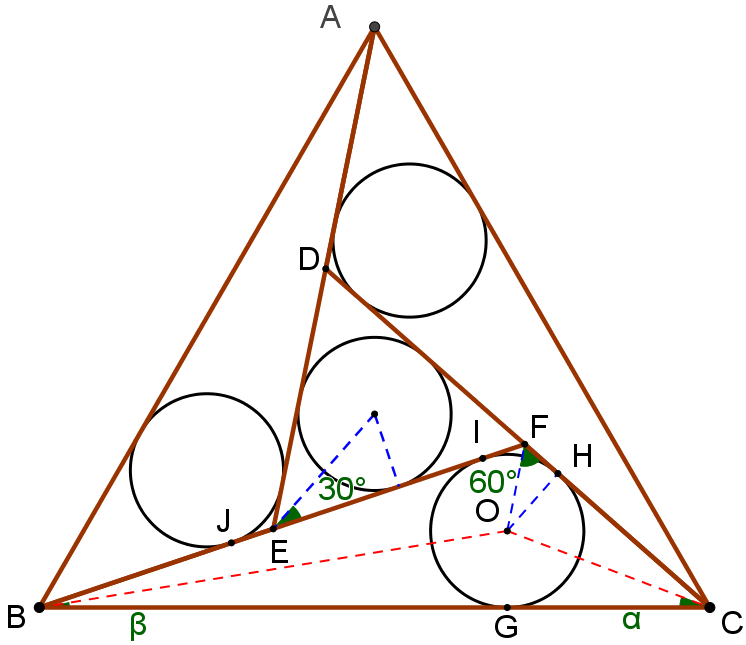
let r be the radius of the circle Δ D E F is equilateral ⇒ ∣ E F ∣ = 2 r 3 ∣ H F ∣ = ∣ J E ∣ = 3 r ∣ B J ∣ = ∣ C H ∣ = ∣ C G ∣ ∣ B G ∣ = ∣ B I ∣ = ∣ B J ∣ + ∣ J E ∣ + ∣ E F ∣ − ∣ I F ∣ ∣ B G ∣ = ∣ C G ∣ + 3 r + 2 r 3 − 3 r = ∣ C G ∣ + 2 r 3 ∣ B C ∣ = ∣ B G ∣ + ∣ G C ∣ 8 = ∣ C G ∣ + 2 r 3 + ∣ C G ∣ ⇒ ∣ C G ∣ = 4 − r 3 ∣ B G ∣ = 4 + r 3 β = ∠ G B O = ∠ I B O α = ∠ H C O = ∠ O C G α + β = 3 0 ° tan ( α ) = 4 − r 3 r tan ( β ) = 4 + r 3 r tan ( α + β ) = 1 − tan ( α ) tan ( β ) tan ( α ) + tan ( β ) tan ( 3 0 ° ) = 1 − 4 − r 3 r ⋅ 4 + r 3 r 4 − r 3 r + 4 + r 3 r 3 1 = 1 6 − 4 r 2 8 r ⇒ r 2 + 2 3 r − 4 = 0 r = − 3 ± 7 r = 7 − 3
Let AD =x then DF=2(√3)r
8-x+r/√(3) = x+2 √(3) r - r/√(3)
Apply co-sine rule in triangle ADC (angle ADC=120°)
(x+2 √(3) r)²+x²+x (x+2√(3) r)=64
r= √7 –√3