3-5-7 square point
Let A B C D be a square. P is a point inside the square such that A P = 3 , P B = 7 and P D = 5 . Find the area of A B C D .
The answer is 58.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
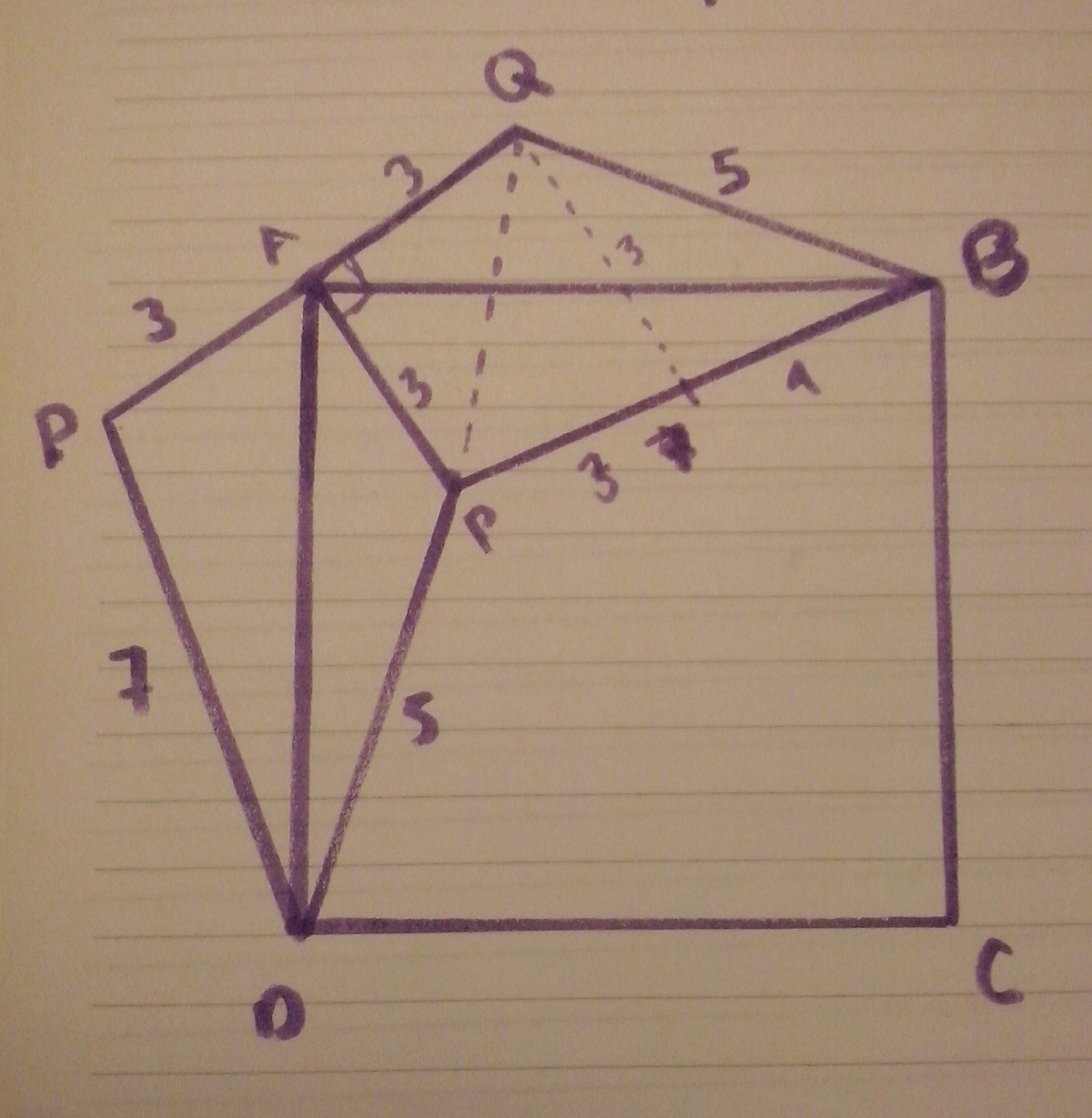
Let △ A Q B ≅ △ A P D the A Q = A P = 3 and ∠ P A Q = 9 0 ° .
As △ A P Q is isosceles ∠ A P Q = 4 5 °
Then by law of cosines proof that ∠ Q P B = 4 5 ° so ∠ A P B = 9 0 ° . \ △ A P B is rectangle and A B is its hypotenuse, and A B C D area is A B 2 ∴ A P 2 + P B 2 = 3 2 + 7 2 = A B 2 = 5 8
How do you prove that angle QPB=45?
Have that P B = 7 , Q B = 5 and Q P = 3 2 (because △ Q A P is rectangle).
We can use law of cosines
5 2 = ( 3 2 ) 2 + 7 2 − 2 ( 3 2 ) ( 7 ) cos ∠ Q P B
2 5 = 1 8 + 4 9 − 2 ( 3 2 ) ( 7 ) cos ∠ Q P B
− 4 2 = − 2 ( 3 2 ) ( 7 ) cos ∠ Q P B
1 = 2 cos ∠ Q P B
∴ ∠ Q P B = 4 5 °
Thanks. I appreciate the explanation.
I will firstly label a few points of interest on the picture:
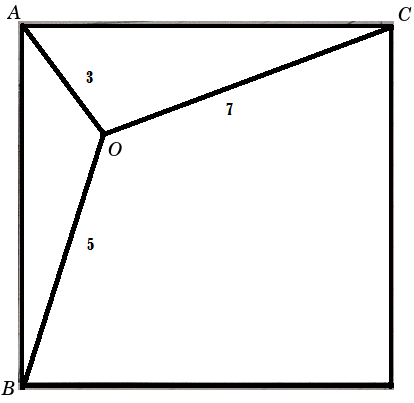
Let us call the angle ∠ O A B = θ , and thus since ∠ C A B = 9 0 ∘ , we find that angle ∠ O A C = 9 0 ∘ − θ . Also, let l be the size of the side of the square.
Firstly, applying the law of cosines on the triangle △ O A B with respect to the side O B will yield the following:
5 2 = 3 2 + l 2 − 2 ∗ 3 ∗ l ∗ c o s ( θ )
6 l ∗ c o s ( θ ) = l 2 − 1 6
c o s ( θ ) = 6 l l 2 − 1 6
Now, applying the law of cosines on the triangle △ O A C with respect to the side O C will yield the following:
7 2 = 3 2 + l 2 − 2 ∗ 3 ∗ l ∗ c o s ( 9 0 ∘ − θ )
6 l ∗ c o s ( 9 0 ∘ − θ ) = l 2 − 4 0
c o s ( 9 0 ∘ − θ ) = 6 l l 2 − 4 0
Thus, we can write:
s i n ( θ ) = 6 l l 2 − 4 0
Now, applying the trigonometric identity s i n 2 ( θ ) + c o s 2 ( θ ) = 1 , we will obtain:
3 6 l 2 l 4 − 3 2 l 2 + 2 5 6 + 3 6 l 2 l 4 − 8 0 l 2 + 1 6 0 0 = 1
2 l 4 − 1 4 8 l 2 + 1 8 5 6 = 0
l 4 − 7 4 l 2 + 9 2 8 = 0
Completing the square:
l 4 − 7 4 l 2 + 1 3 6 9 = 4 4 1
( l 2 − 3 7 ) 2 = 2 1 2
So, either l 2 − 3 7 = 2 1 , which gives us l 2 = 5 8 , or l 2 − 3 7 = 2 1 , which gives us l 2 = 1 6 . l 2 cannot be equal to 1 6 because if it were, then l = 4 , and this would imply that the triangle △ O A C is degenerate since the triangle inequality wouldn't hold, given that 3 + 4 > 7 is false. Thus, l 2 = 5 8 , which so happens to be the area of the square.
Applying Law of Cosines three times on triangles △ A P B , △ A P D and B P D we get if we let A P = a , B P = b , D P = c and A B = L :
L 2 = 2 b 2 + c 2 + ( 2 b c ) 2 − ( b 2 + c 2 − 2 a 2 ) 2
Substitute the known values:
L 2 = 2 b 2 + c 2 + ( 2 b c ) 2 − ( b 2 + c 2 − 2 a 2 ) 2 L 2 = 2 7 2 + 5 2 + ( 2 ⋅ 7 ⋅ 5 ) 2 − ( 7 2 + 5 2 − 2 ⋅ 3 2 ) 2 L 2 = 2 7 4 + 1 7 6 4 L 2 = 5 8
how you got first. how you applied cosine rule 3 times on triangles
He used cosine rule each for the three triangles and then formed a relation between them
Can u plz show which one is triangle APB, APD, BPD. In the ques there is nothing labelled
Let the side length of the square A B C D be a and A be ( 0 , a ) , B ( a , a ) , C ( a , 0 ) , D ( 0 , 0 ) and P ( x , y ) .
Then, we have:
⎩ ⎪ ⎨ ⎪ ⎧ P D 2 : x 2 + y 2 = 2 5 A P 2 : x 2 + ( a − y ) 2 = 9 P B 2 : ( a − x ) 2 + ( a − y ) 2 = 4 9 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
⎩ ⎪ ⎨ ⎪ ⎧ E q . 1 − E q . 2 : − a 2 + 2 a y = 1 6 E q . 3 − E q . 2 : a 2 − 2 a x = 4 0 y = 2 a a 2 + 1 6 x = 2 a a 2 − 4 0
Substituting x and y in E q . 1 :
⇒ ( 2 a a 2 − 4 0 ) 2 + ( 2 a a 2 + 1 6 ) 2 = 2 5 ⇒ a 4 − 7 4 a 2 + 9 2 8 = 0
⇒ a 2 = 2 7 4 ± 7 4 2 − 4 ( 9 2 8 ) = 2 7 4 ± 4 2 = 5 8 or 1 6 but a > 4 .
Therefore, the area of A B C D = a 2 = 5 8 .