Equilateral triangle and two congruent circles!
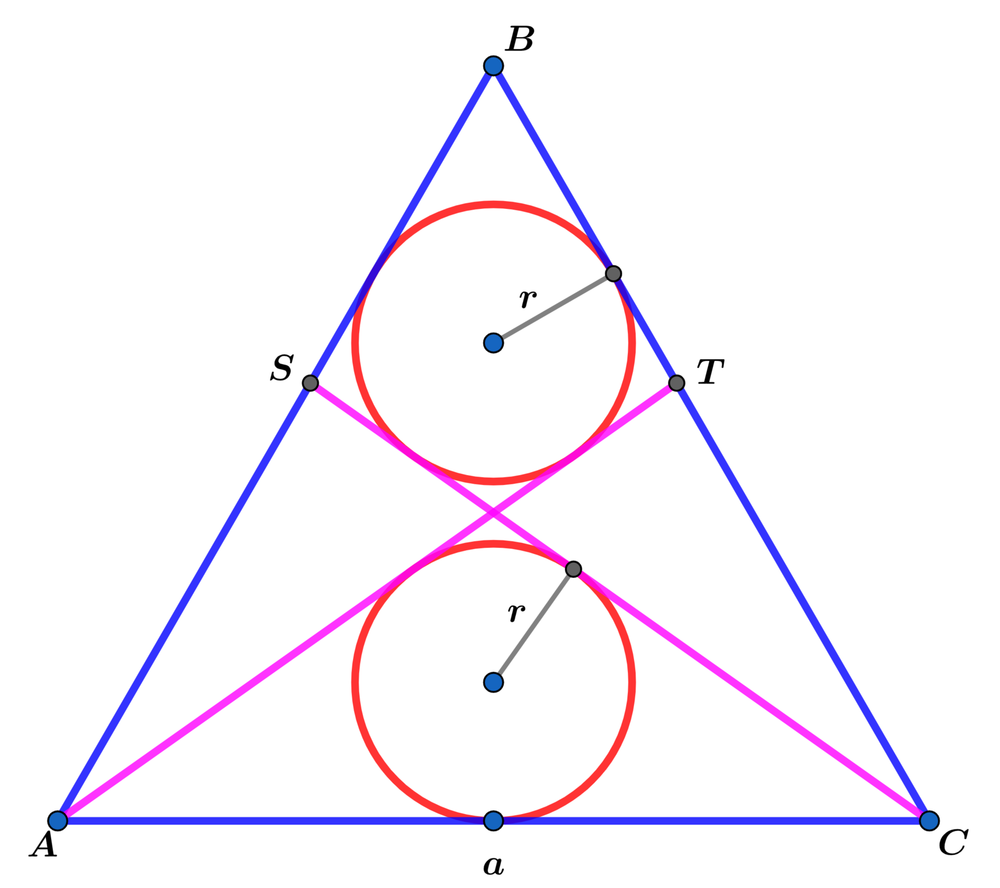
In equilateral △ A B C with side length a , C S and A T are tangent to the two circles each with radius r and A B and B C are tangent to the upper circle and A C is tangent to the lower circle as shown above.
If a r = β α − β , where α and β are coprime positive integers, find α + β .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the equilateral triangle have a side of 2, and it's obvious in a glance that the height is 3r + 2s, with 2s the distance between the two incenters and s the distance between one of them to the intersection point of two pink lines.
s² – r² = [(2 – √3r) – (2 / 1)]² / 4
= (1 – √3r)² / 4
4s² = 7r² – 2√3r + 1
√3 = 3r + 2s
= 3r + √(7r² – 2√3r + 1)
7r² –2√3r + 1 = (√3 – 3r)²
= 9r² – 6√3r + 3
0 = 2r² – 4√3r + 2
= r² – 2√3r + 1
(r – √3)² = 2
r = √3 ± √2
3r < √3
r = √3 – √2
r / a = (√3 – √2) / 2
Answer = 3 + 2 = 5
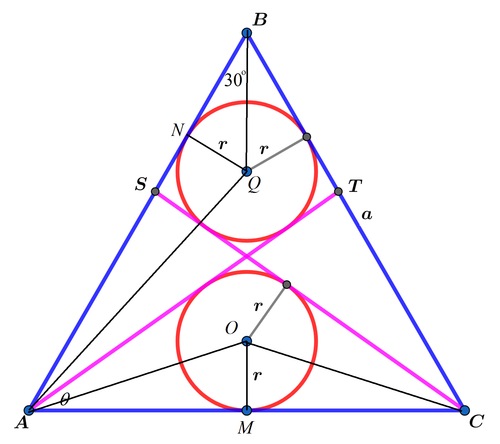
Let the centers of the lower and upper circlers be O and Q respectively, O M and Q N be perpendicular to A C and A B respectively, and ∠ T A C = ∠ S C A = θ . Using the fact that the line joining a vertex and incenter bisects the vertex angle,
A N + N B Q N cot 2 ∠ T A B + Q N cot 3 0 ∘ r cot ( 3 0 ∘ − 2 θ ) + r cot 3 0 ∘ 1 − 3 t 3 + t ⋅ r + 3 r = A B = A B = a = a Let t = tan 2 θ
Similarly for A C , we have t 2 r = a . Then
1 − 3 t 3 + t + 3 1 − 3 t 3 + t 2 t 2 − 4 3 t + 2 t 2 − 2 3 t + 1 ⟹ t = t 2 = t 2 − 3 t = 0 = 0 = 3 − 2 For θ < 9 0 ∘
Since t 2 r = a , ⟹ a r = 2 t = 2 3 − 2 . The required answer α + β = 3 + 2 = 5 .
△ B M C ∼ △ B O D ⟹ 2 B D 3 a = 2 r a ⟹ B D = 3 r
⟹ D C = a − 3 r = C E ⟹ △ E O C ≅ △ D O C by s . a . s
and vertical angles ∠ O P E ≅ ∠ Q P O ′ ⟹ △ E O P ≅ △ P O ′ Q by a . a . s
and C Q ≅ C M = 2 a ⟹ △ C Q O ′ ≅ △ C O ′ M by s . a . s
⟹
A △ B M C = 8 3 a 2 = A △ B O D + 2 A △ D O C − A △ E O P + A △ P O ′ Q + 2 A △ Q O ′ C
= 2 3 r 2 + ( a − 3 r ) r + 2 a r ⟹ 3 a 2 = 1 2 a r − 4 3 r 2 ⟹
4 3 r 2 − 1 2 a r + 3 a 2 = 0 ⟹ r = 2 a ( 3 ± 2 ) and for
r = 2 a ( 3 + 2 ) ⟹ a − 3 r < 0 ∴ we choose r = 2 a ( 3 − 2 )
⟹ a r = 2 3 − 2 = β α − β ⟹ α + β = 5 .