Equilateral Triangle Dissection
An equilateral triangle
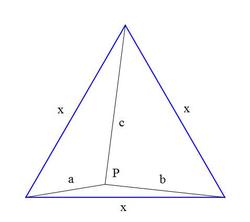
has an interior point from which the distances to the vertices are distinct integers that satisfy the condition
where the notation shall denote the non-zero area of a triangle with sides , and is the side of the equilateral triangle.
Find the minimum value can have.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For any P this condition
2 Δ x x x = Δ a a a + Δ b b b + Δ c c c + 3 Δ a b c
is always true, because it's a geometrical identity. Hence, we examine the first few possible sets
{ 1 , 2 , 3 } , { 1 , 2 , 4 } , { 1 , 2 , 5 } , { 1 , 3 , 4 } , { 2 , 3 , 4 }
and then rule out
{ 1 , 2 , 3 } because the point P is outside the equilateral triangle
{ 1 , 2 , 4 } , { 1 , 2 , 5 } because no point P is possible with those distances
{ 1 , 3 , 4 } because Δ 1 3 4 is zero, leaving
2 + 3 + 4 = 9 as the smallest possible answer meeting all conditions.
The figure for this answer is already given at the start of this problem.
Proof of this geometrical identity can be found through dissections. The following graphic suggests how this may be done.