Equilateral Triangle Geometry
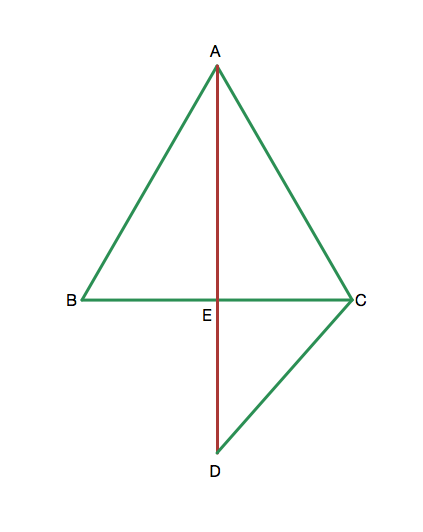 The equilateral triangle ABC has a height from A, which intersects BC at E. Extend AE to a point D such that AC=CD. Find the angles EBD and EDB in degrees.
The equilateral triangle ABC has a height from A, which intersects BC at E. Extend AE to a point D such that AC=CD. Find the angles EBD and EDB in degrees.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
how internal angles are 60 degree ?????????????
Log in to reply
Because it's an equilateral triangle, in every equilateral triangle, i.e. an triangle which all sides has the same length, all angles are 60. Try to make an equilateral triangle with different angles, it's completely impossible.
because its an equilateral triangle ..... in an equilateral triangle all sides are equal and hence all angles are equal... as sum of all angles in a triangle is 180 degrees x+x+x=180=> 3x=180=> x=180/3=>x=60
Definition of an equilateral triangle that is bisected from the vertex to the base: it's a 30-60-90 triangle.
the diagram is not reliable..
it is equilateral triangle
its simple qbc is equilateral so<ace=60 degree and ad is the perpendicular bisector of bc so <aec=90degree so <eac=180-(90+60)=30. now since ac=dc so <cde=30 degree and triangle edc &bed are congurent so <ebd=180-(90+30)=60
how <ace=60 degree ?????????????????
it is equilateral triangle , all angles are equal , and its sum equal to 180
how <ebd=60 explain how u applied congruency??
The equilateral triangle has all 3 inside angles equal to 60° each. By extending the height AE which intersects the side BC in the middle, to a point D so that AC=CD, we draw exactly an other equilateral triangle opposite the first one. The right triangle AEC is congruent to the right triangle DEC ( 2 right triangles having their hypothenuses equal, are equal, congruent). So AE= ED, AC=CD, EC is shared. Therefore Triangle ABC=triangle DBC. Therefore the triangle DBC is equilateral and all inside angles are 60°. The height AE intersect the angle BAC in 2 halves, so does also the height DE which intersect the angle CDB in 2 halves, therfore the angle EDB=30°, and the angle DBC is 60° (inside angle of an equilateral triagle) which is also equal to EBD.
Half an equilateral triangle makes a 90-60-30 right triangle, which would be △ A E C , since it is the side we are dealing with.
If A C = C D , that means that △ B C D is equilateral, because of Hypotenuse-leg theorem (EC and EC because of reflexive property (leg), DC and AC due to the problem (hypotenuse), and ∠ D E C and ∠ A E C , since I have proven the latter is 9 0 ∘ , and when a line separates a straight line, the resulting angles are supplementary (the theorem only works for right triangles, so...)).
So the angle split by the altitude ( ∠ B D E ) would be 3 0 ∘ because of the type of right triangle created here, and the other angle would obviously be 6 0 ∘ because of the Triangle Sum Theorem 1 8 0 − ( 9 0 + 3 0 ) = 6 0 ∘
Side EC is common & given AC=CD. Since the picture is not drawn to scale, there appears to be some confusion . How ever Triangles AEC & CED are identical . similarly when points B&D are joined u find a mirror image of Triangle ECD. Hence angle EBD=ECD=ACE=60 degrees. andAngle EBD is 30 degrees
Since details given are showing that anle ABE is 60 degree so angle EBD will be 60.also AE is bisecting angle A so it is 30 degree and therefore angle EDB is also 30 degree.Ans. K.K.GARG,India
its simple sum of all angles of a triangle is equal to 180.... angle BED is of 90 degrees and AD is a bisector line which divides angle to two equal parts so...through this angle BDE is 30 and the other angle is of 60 degree
The key words here are "height from A", which means AE is perpendicular to BC. For an equilateral triangle, that means AE bisects BC and so we have symmetry all the way around with sides AB=AC=CD=BD and angle BAC bisected. So angle BAE = angle EDB = 30. That leaves angle EBD = 60, because angle DEB = 90.
Its very simple - you extend AE so that AC = CD - these are both sides of the triangles.
This means that Triangles ABC and BCD are constructed of sides of equal length, so they are both equilateral and all internal angles are 60.
EBD is therefore 60, and EDB is half of an internal angle and hence 30.