Equilateral Triangle Property
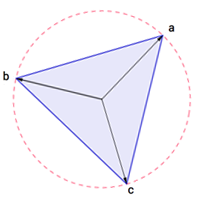
Let be a , b and c three complex numbers such that ∣ a ∣ = ∣ b ∣ = ∣ c ∣ . The affix of these three complex numbers are the vertices of an equilateral triangle.
What is the value of a + b + c ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Good observation that b = ω a by the multiplication of complex numbers.
We can even do this in the following way.Since in equilateral triangle circumcentre(represented by 0 in argand plane) and centroid are the same point therefore (a+b+c)/3=0.Hence a+b+c=0.
Let be a , b and c the complex numbers and their affixes are vertices of an equilateral triangle. They verify that
b = 1 1 2 0 ∘ ⋅ a and c = 1 2 4 0 ∘ ⋅ a . The affixes of b and c are the result of rotating the affix of a the angles 1 2 0 ∘ and 2 4 0 ∘ respectively.
And we have
a ⋅ a − 1 = 1 , b ⋅ a − 1 = 1 1 2 0 ∘ , c ⋅ a − 1 = 1 2 4 0 ∘ .
If ω denote ω = b ⋅ a − 1 ⇒ w 2 = c ⋅ a − 1 and w 3 = 1 = a ⋅ a − 1 .
Then { 1 , ω , ω 2 } are roots of the polynomial z 3 − 1 .
Using the Cardano-Vieta formulas we have that the sum of the three roots is equal to the opposite of the grade 2 monomial coefficient of the polynomial z 3 − 1 .
So 1 + ω + ω 2 = 0 due to 0 is the coefficient of z 2 monomial.
Then
a ⋅ a − 1 + b ⋅ a − 1 + c ⋅ a − 1 = 0 ⇒
( a + b + c ) ⋅ a − 1 = 0 and a = 0 ⇒
| a + b + c = 0 |
If ω = e 2 π i / 3 , then ω ( a + b + c ) = ( b + c + a ) so ( ω − 1 ) ( a + b + c ) = 0 and a + b + c = 0