Equilateral Triangles

Geometry Level 2

Let a a be the area of an equilateral triangle, and let b b be the area of another equilateral triangle inscribed in the incircle of the first triangle. What is a b \frac{a}{b} ?


The answer is 4.

L S by l s , 23, Canada

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

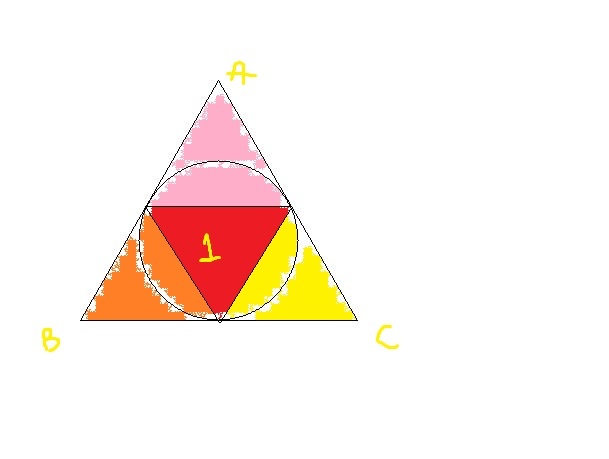
After drawing the larger triangle and the incircle, join the three resulting points of tangency to form a triangle. By symmetry, this (inverted) inscribed triangle is also equilateral, and each side of this triangle is shared by another equilateral triangle within the larger triangle. As a result, the larger triangle has been divided into four congruent equilateral triangles, implying that a b = 4 \frac{a}{b} = \boxed{4} .

10 Helpful 0 Interesting 0 Brilliant 0 Confused

Maybe you could give a more sound answer by means of calculations...

Aditya Singh - 4 years, 3 months ago
Syed Hissaan
Feb 21, 2017

as it can be seen that the area 1 is 1 / 4 1/4 of the total so answer is 4 / 1 = = > 4/1 ==> 4

3 Helpful 2 Interesting 0 Brilliant 0 Confused

Since the smaller equilateral triangle's circumradius will be equal to the larger equilateral traingle's inradius the side of the larger equilateral triangle will be in the ratio of 2:1 with the side of the smaller equilateral triangle (Because Circumradisu : Inradius is 2:1). Area of any equilateral triangle will be proportional to the square of its side so the ratio of Area of larger equilateral triangle (a) : Area of Smaller equilateral triangle (b) will be 2^2 : 1 i.e. 4:1

Nirat Patel - 1 year, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...