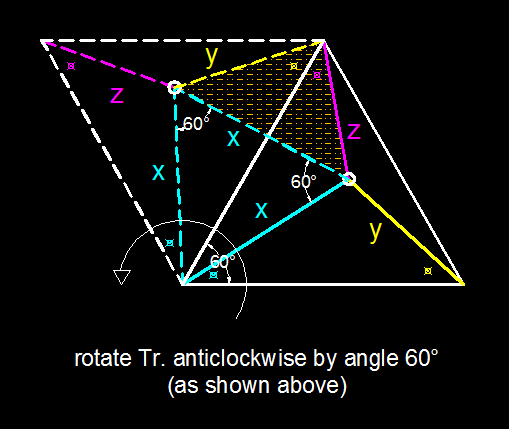
Equilateral

Geometry Level 2

As shown in the diagram, a blue point is randomly chosen inside an equilateral triangle. The distances between the blue point and each of the vertices are $x, y, z$ .

Is the following statement true or false?

There exists a triangle with side lengths $x, y, z$ .

Always true Only sometimes true Never true

2 solutions

Ahmad Saad
Jul 10, 2017

Interesting, but whatever 3 (non-null) lengths they'll always form a triangle, so what's the buzz?!

Horia Tudosie - 3 years, 10 months ago

For point inside equilateral triangle:

any distance X , y or Z is less than triangle side length.

any some of of two distances (X+Y),(Y+Z) or (Z+X) are greater than triangle side length.

then distances X,Y and Z form a triangle (Triangle Inequality Theorem).

Are you mean that?

Ahmad Saad - 3 years, 10 months ago

I know I was wrong (and stupid.) I have put the comment after midnight, I've woke up knowing you cannot make a triangle from 10,1,1. Triangle inequality from metric space - of course!

Horia Tudosie - 3 years, 10 months ago

Vincent Huynh
Jul 18, 2017

x+y >= Triangle Size >= z x+z >= Triangle Size >= y y+z >= Triangle Size >= x

these are enough to confirm that x,y,z can be sides of a triangle

Equilateral

2 solutions

0 pending reports