Equilibrium of JEE!
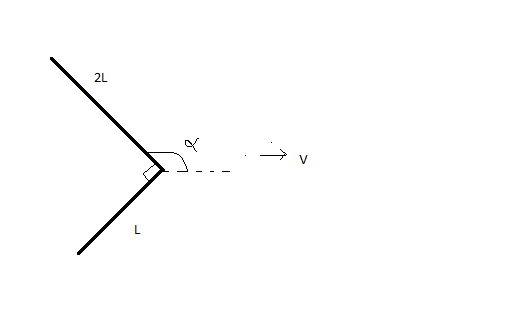 A straight metal rod of length
3
L
is bent through the right angle as shown. The bent rod is then placed on a
rough horizontal table
. A light string is attached to the vertex of the right angle. The string is then pulled horizontally so that rod slides at a constant velocity
v
.
A straight metal rod of length
3
L
is bent through the right angle as shown. The bent rod is then placed on a
rough horizontal table
. A light string is attached to the vertex of the right angle. The string is then pulled horizontally so that rod slides at a constant velocity
v
.
Find the angle α (in degrees ) that the side 2 L would make with the string.
Details and Assumptions
- Mass density of rod: ρ r = 1 0 kg/m ,
- Length: L = 1 0 m ,
- Velocity: v = 1 0 m/s .
This is asked in very old IIT JEE exam !
The answer is 165.96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Good one !!
Did the same.
Brilliant Solution!
Write a comment or ask a question...
Did same thing.
That's trivial.But nice...
Let
λ
to be linear mass density so
according to figure
 Figure
f
2
=
2
μ
λ
L
g
f
1
=
μ
λ
L
g
.
Figure
f
2
=
2
μ
λ
L
g
f
1
=
μ
λ
L
g
.
Now Rod is in equilibrium : ∵ τ o , n e t = 0 . f 2 L sin α = f 1 2 L sin ( α − 2 π ) α = π − tan − 1 4 1 = 1 6 5 . 9 6 d e g r e e .
same way, except used integration to evaluate torque :)
I did in similar manner but rechecked my answer twice as it come independent of any data given in question
Log in to reply
I Put Dummy Values to this Question ! But In original JEE question data is not given ! :)
Log in to reply
How can such a easy problem be level 5. Thats the worst side of brilliant.
I think f1 and f2 are reversed in fig as per your explaination. Perhaps obvious!
Did the same way
i also did this problem by using this method
Did the same but what is the use of the given data I nowhere required it.
Exactly !! :) ( same way)
did the same !!!!!
Method 1
As the rod is moving with constant velocity, we can safely write the torque equation relative to any point on the rod (without bothering about the torque of pseudo force). The most convenient point is the right angled vertex.
λ ( 2 L ) g ( L sin ( π − α ) ) = λ L g ( L cos ( π − α ) ) ⇒ tan α = − 4 1
⇒ α ≈ 1 6 6 deg
Method 2
The centre of mass must lie along the line of the thread. Treating the two rods as point masses located at their respective CMs, we can say that the CM must divide the line joining them in the inverse ratio of masses.
2 L cos ( π − α ) L sin ( π − α ) = 2 1 ⇒ α ≈ 1 6 6 deg
well Your Torque equation about right angled in Method-1 is wrong
Log in to reply
Yes ... thanks ... the RHS should be λ L g ( 2 L cos ( π − α ) )
I think all we need to do is that Centre of mass must lie in line of force.
Since mass density is constant, Mass of 2L=2M and mass of L=M, Now 2 M ( L s i n α ) = M 2 L c o s α ⇒ t a n α = 0 . 2 5 .
Here I have assumed α the angle between horizontal and 2L, so our answer will be 180-arctan 0.25=165.96 degrees!