Equilibrium: stable or unstable, that is the question...
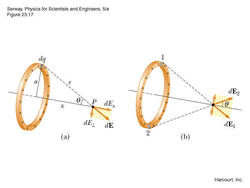 A uniformly charged ring of radius
with linear charge density
lies on the ground. Above it, along its axis, hovers a particle of mass
and charge
. The particle is in equilibrium.
A uniformly charged ring of radius
with linear charge density
lies on the ground. Above it, along its axis, hovers a particle of mass
and charge
. The particle is in equilibrium.
Describe the equilibrium of the particle:
(i) If the separation between the charged particle and the centre of the ring is less than
(ii) If the separation between the charged particle and the centre of the ring is greater than
Details & Assumptions
- The ring retains its charge; it is not lost to the ground.
- A uniform gravitational field is acting downward.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For a ring, the maximum Electric Field Intensity is at d = 2 R where d is the distance from the centre of the ring.
In case (i), if the particle is slightly pushed forward, it would experience more force, hence unstable.
In case (ii), if the particle is slightly pushed forward, it would experience less force, hence stable.