Equipotential Spheres
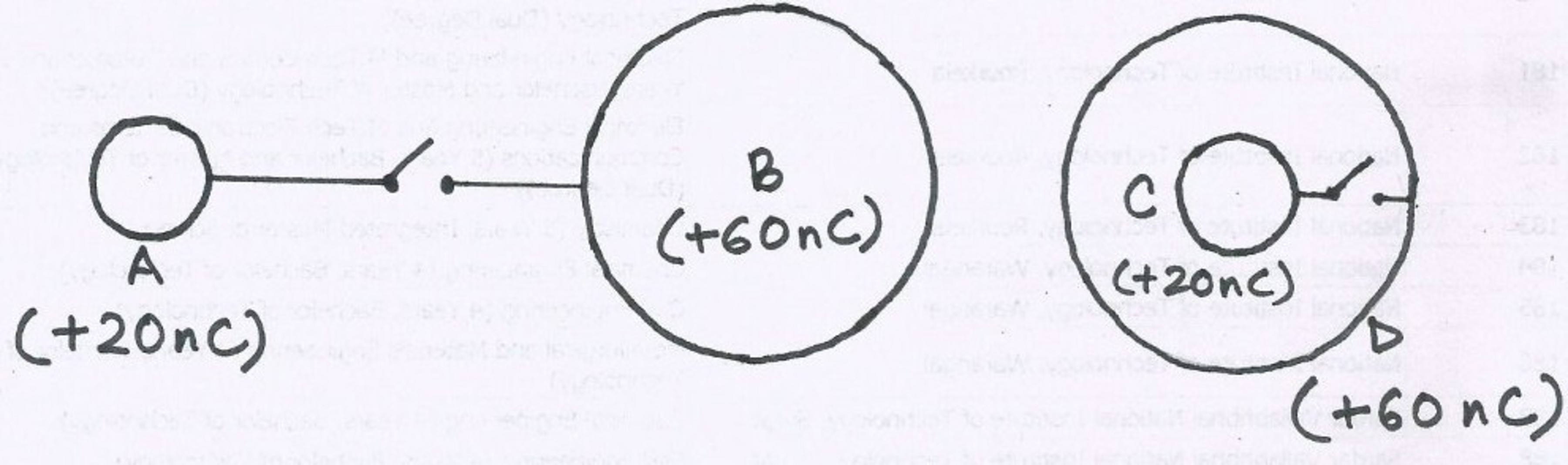
Two pairs of hollow, spherical conducting shells are connected with wires and switches. The system (where and are far apart) is extremely far from . In both systems the large shells have four times the radius of the small shells. Before the switches are closed each pair has a charge of on the smaller shell ( , ) and on the large shell ( , ).
When the switches are closed, charge is free to flow along the conducting wires connecting the spherical shells. What is the rank of magnitude of the charge on each of the shells after the switches have been closed ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For the first system consisting of spheres A and B, charge will redistribute on the basis of the capacitance of each spherical conductor. Capacitance of an isolated spherical conductor is:
C = 4 (pi) (epsilon) R where R is radius of the sphere.
Since radius of B = 4 * radius of A, the total charge will also be distributed in this ratio.
For the system of shells C and D, all the charge must shift to D for the two surfaces to be at the same potential, since any charge on C would create a radial electric field between C and D which would lead to a potential difference.