Equivalent Capacitance

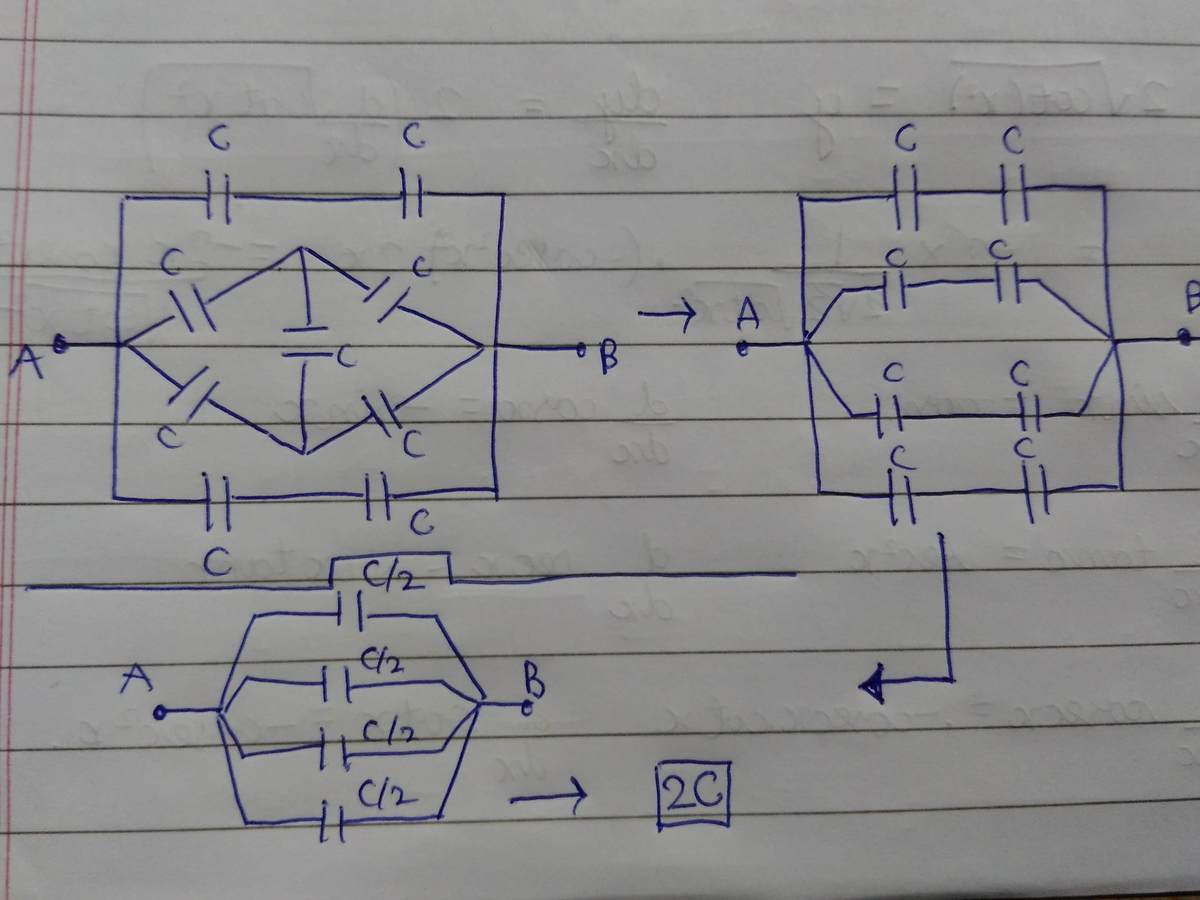
Due to symmetry of the circuit the middle vertical capacitor has the same potential on both plates and hence zero voltage across and no difference in charges on two plates. This means that the middle vertical capacitor can be considered an open circuit or close circuit, therefore the equivalent capacitance is as follows:

1) Considering the middle capacitor as an open circuit, then there are four $\times$ two capacitors $C$ in series.

$\begin{aligned} \quad C_{AB} & = (C \color{#3D99F6}{\oplus} C) \color{#3D99F6}{||} (C \color{#3D99F6}{\oplus} C) \color{#3D99F6}{||} (C \color{#3D99F6}{\oplus} C) \color{#3D99F6}{||} (C \color{#3D99F6}{\oplus} C) & \small \color{#3D99F6}{\oplus = \text{series, } \ || = \text{parallel}} \\ & = 4 \times \frac {C\times C}{C+C} = 4 \times \frac C2 = \boxed{2C} \end{aligned}$

2) Considering the middle capacitor as a close circuit,

$\begin{aligned} \quad C_{AB} & = (C \oplus C) || [(C || C ) \oplus (C || C)] || (C \oplus C) \\ & = \frac C2 + \left[2C \oplus 2C \right] + \frac C2 \\ & = \frac C2 + C + \frac C2 = \boxed{2C} \end{aligned}$

This problem can also be solved by simplification using wheatstone bridge circuit as shown $4\times \dfrac C2=\boxed{2C}$