Equivalent capacitance

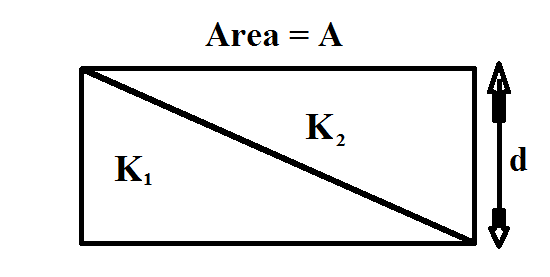
According to the figure The right vaccum place is filled by dielectric constant $K_1$ & the left above vaccum by dielectric constant $K_2$

Let us consider the capacitance of the slab whose width is 'b' & length 'dx & seperation 'y' be $dC_1$ & the above slab whose separation is (d-y) be $dC_2$ .

Now Area of the those two slabs is = $b.dx$

$\displaystyle \begin{aligned} dC_1 = \frac{\epsilon_0AK_1}{y} \end{aligned}$

$\displaystyle\begin{aligned} dC_2 = \frac{\epsilon_0AK_2}{d-y} \end{aligned}$

$\text{Since they are connceted in series we have their equivalent capacitance dC}$

$\displaystyle\frac{1}{dC_1} + \frac{1}{dC_2} = \frac{1}{dC}$

$\displaystyle\frac{1}{dC} = \frac{1}{\epsilon_0A}(\frac{y}{K_1} + \frac{d-y}{K_2})$

$\displaystyle\frac{1}{dC} = \frac{1}{\epsilon_0AK_1K_2}(dK_1 + y(K_2-K_1))$

$\displaystyle dC = \frac{\epsilon_0AK_1K_2}{(dK_1 + y(K_2-K_1))}$

$\text{So the entire capacitance over length 'l' is given by :}$

$\displaystyle C = \int_{0}^{l} \frac{\epsilon_0AK_1K_2}{(dK_1 + y(K_2-K_1))}$

We have from figure that $A=b.dx$ & $tan\theta = \frac{y}{x} = \frac{d}{l} \implies y = x\frac{d}{l}$

$\displaystyle C = \int_{0}^{l} \frac{\epsilon_0bK_1K_2}{(dK_1 + x\frac{d}{l}(K_2-K_1))}dx$

$\displaystyle C = \int_{0}^{l} \frac{\epsilon_0bK_1K_2l}{d(K_1l + x(K_2-K_1))}dx$

$\displaystyle C = \frac{\epsilon_0bK_1K_2l}{d} \int_{0}^{l}\frac{1}{(K_1l + x(K_2-K_1))}dx$

$\displaystyle C = \frac{\epsilon_0bK_1K_2l}{d} \frac{1}{K_2-K_1}(log|K_1l + x(K_2-K_1)|)_{0}^{l}$

$\displaystyle C = \frac{\epsilon_0bK_1K_2l}{d} \frac{1}{K_2-K_1}(log|\frac{K_2}{K_1}|)$

$\displaystyle C = \frac{\epsilon_0bK_1K_2l}{d(K_2-K_1)}(log|\frac{K_2}{K_1}|)$

$\displaystyle C = \frac{\epsilon_0AK_1K_2}{d(K_2-K_1)}(log|\frac{K_2}{K_1}|)$

$\text{The final capacitance is C \& putting values thus provided we derive } \boxed{\color{#624F41}{\mathbf{C=9.163}}}$