Equivalent Resistance (1)

We know that the current prefers a low resistance path and if it is to travel between two points, then greater current will travel through the path will smaller resistance. If there is a zero resistance path between the two points, then all the current will flow through that path and the all the parallel paths will be considered short-circuited.

A similar situation occurs in this problem.

There exist a zero resistance path between points $C$ , $D$ and $E$ , $F$ . Hence the current will flow as follows.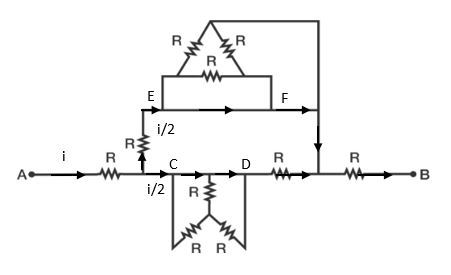

This leaves us with the following equivalent circuit.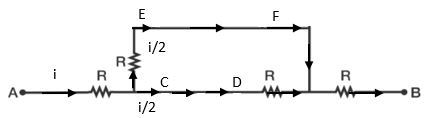

Now, applying series and parallel combinations, we get $R_{eq} = 2R + \dfrac{R}{2} = \dfrac{5R}{2} = 2.5R$ .