Equivalent resistance 5
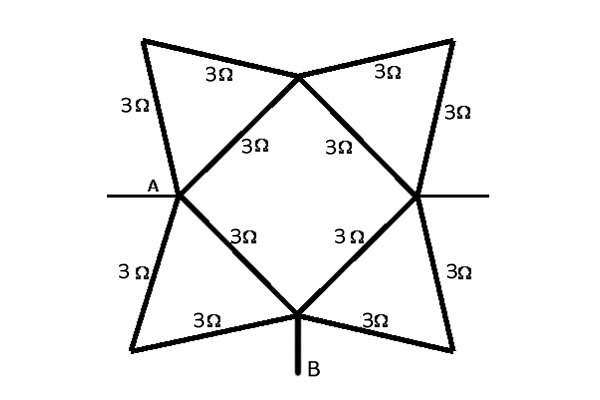 Find the equivalent resistance between points
A
and
B
.
Find the equivalent resistance between points
A
and
B
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Every triangular circuit of 3 × 3 Ω resistors connected at two apexes is actually a parallel circuit of 3 Ω + 3 Ω and 3 Ω or 6 Ω / / 3 Ω = 2 Ω .
Therefore, the equivalent resistance R e q = ( 2 Ω + 2 Ω + 2 Ω ) / / 2 Ω = 6 Ω / / 2 Ω = 6 + 2 6 × 2 Ω = 1 . 5 Ω
The given circuit can be rearranged as follows:
 Alt text
Alt text
The equivalent resistance will be 1 . 5 o h m s
Take any triangle, the base of each triangle(which is the side of a square) is parallel to the other two resistors on the other sides of the triangle. The resultant of each triangle is 2 ohms. The three sides of square are parallel to side ab. The net resistance is 1.5 ohms.
each triangular part has 3 3ohm resistance out of which 2 are in series and one is in parallel so Req for each triangle=2ohm now there are 3 triangles in series which are parallel to one triangle so R1=3x2ohm = 6ohm Rtotal=6x2/(6+2)=3/2=1.5ohm