Escalating x -er
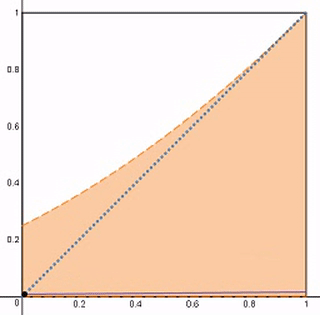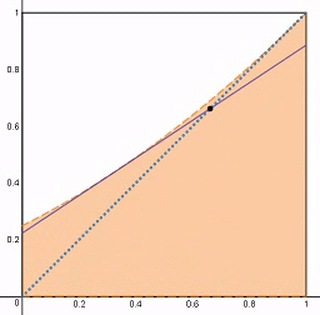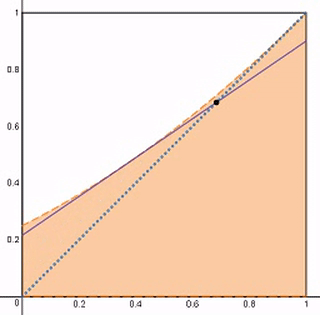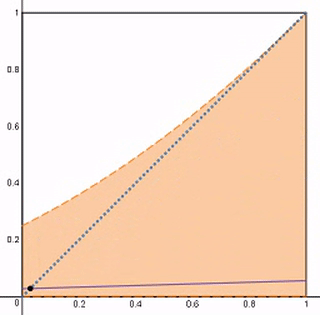
The straight purple line—intersecting the line y = x at the marked points ( x , x ) —has a varying slope of x throughout the move. As shown, the orange region is formed within the unit square.
Given that the area of the orange region is A , input ⌊ 1 0 0 0 A ⌋ as your answer
The answer is 583.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let t denote the parametric variable of the purple line. Then, its equation is y ( x , t ) = t ( x − t ) + t = t x + ( − t 2 + t ) = − t 2 + t ( x + 1 ) Since the intersection points of both orange boundary and purple line are the highest peak points (thus global maxima) of all parabolas with respect to t , quadratic formula shows that t = 2 x + 1 which gives y ( x ) = − ( 2 x + 1 ) 2 + ( 2 x + 1 ) ⋅ ( x + 1 ) = 4 1 ( x + 1 ) 2 Thus, since A = 0 ∫ 1 4 1 ( x + 1 ) 2 d x = 1 2 7 the answer to the problem is ⌊ 1 0 0 0 A ⌋ = 5 8 3
How did you make the animated picture in the problem? It looks like Desmos but I can't find a way to export anything more than stills.
Edit. Found it: http://www.gifsmos.com/
Log in to reply
First, I created the diagram, using Desmos. Then, I use EZGif to transfer from video format to cropped gif image. :)
The purple line has equation y = a ( x − a ) + a = − a 2 + ( x + 1 ) a where ( a , a ) is the marked point.
To find the highest point at a given x-coordinate note the equation looks like a negative quadratic in terms of a so its vertex is given by a = 2 ⋅ − 1 − ( x + 1 ) = 2 x + 1 .
This is enough to find the equation of the dotted curve by subbing a into the original equation again:
y = 2 1 + x ( x − 2 1 + x ) + 2 1 + x = ( 2 1 + x ) 2
It's just a parabola. The quickest way of finding the area is the integral
∫ 0 1 ( 2 1 + x ) 2 d x = 1 2 7 ≈ 0 . 5 8 3 3 so the solution is 5 8 3