Escape From Trigonometric Maze
You are in room 1 in the upper left corner of a maze of rooms. The goal is to escape this maze and exit through room 2 5 at the bottom right, but you can only move either right or down, passing through a total of 9 rooms.
You need to deliberately find a path to get out exactly the same way you were when you started in room 1 , because each room alters you, sometimes even making you imaginary.
What path will let you do that?
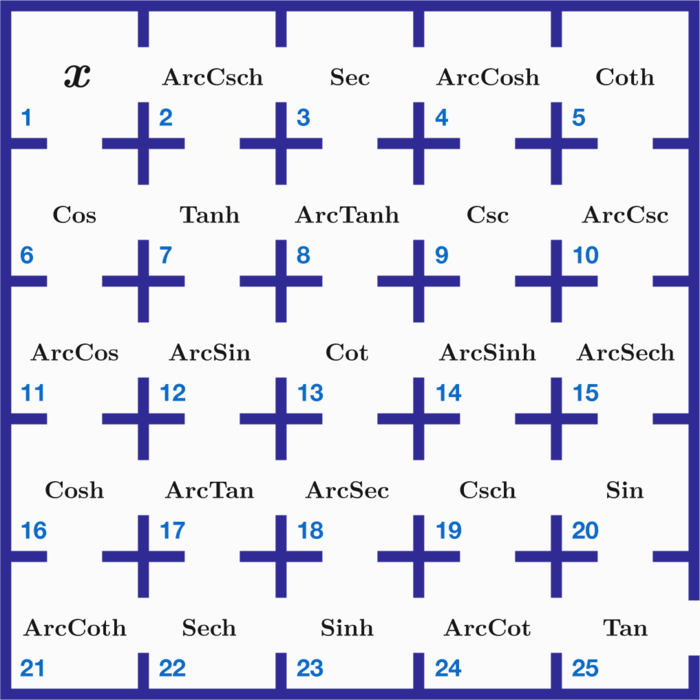
Enter your answer as the total of the room numbers you must pass through in order to do that, a sum of 9 numbers starting with 1 and ending with 2 5 .
For example, if you go through rooms
1
,
2
,
3
,
4
,
5
,
1
0
,
1
5
,
2
0
,
2
5
, the total is
8
5
. However, you will experience the succession of functions
Tan
(
Sin
(
ArcSech
(
ArcCsc
(
Coth
(
ArcCosh
(
Sec
(
ArcCsch
(
x
)
)
)
)
)
)
)
)
)
so that if you started with for example a real value of
0
.
5
,
you would end up being a totally imaginary number
0
.
7
1
4
i
when you leave the maze, which does not fulfill the requirement.
Note:
- x cannot start with i , − i , or 0 for this problem, but can be any other value, real or complex.
- See Gudermannian Function .
The answer is 117.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Solved this using programming (Excel) :
1-Mapped each of the 25 cells with their 0 to 2 possible next cells (25x3 matrix)
2-Created a 1000x9 matrix containing each possible path using random walk (vlookups and conditions used)
3-Had to implement missing math functions such as ACSCH, ACSC, ASECH and ASEC using VBA because they are missing on Excel
4-Initialized a constant to 1 and created a result cell that combines each of the 1000 lines into the targeted functions
5-By an immense miracle, the 1st line generated randomly was the right path to the correct answer 117 (1,2,7,8,13,18,19,24,25)
I can provide the Excel file for the curious minds
For a heuristic in seeking the correct answer, I looked for a path that had equal numbers of "trig and inverse trig" as well as "hyperbolic trig and inverse hyperbolic trig" functions in the appropriate orders such that I could handle "cancelling pairs" from the inside-out as needed (Recognizing that I know identities that allow me to deal with tan(arccos(x)) and arcsinh(cosh(x)) and the like). For example, if we code "trig" as t and "inverse trig" as t − 1 , hyperbolic trig as h and h − 1 likewise, I sought paths which would simplify by cancelling only adjacent terms with opposite powers.
Following a quick color-coding it was quick to see that no such path could travel through blocks 3 or 8 (due to the number of inverse hyperbolic segments "blocking" the rest of the route) or through blocks 16 or 17 for a similar reason with trigonometric functions. This left
It turns out that there were only two such paths to worry about:
1 2 7 12 13 14 19 24 25
and
1 6 11 12 13 14 19 24 25
Checking both of them through identities, as many have demonstrated already, shows that the first is correct. If I end up with the time I might demonstrate exactly which identities in which order yield the "least annoying" computations, but this should be apparent from the "cancellations" above.
My primary reason in writing this solution, which is not a complete solution, is to provide one quick heuristic for looking for candidate paths, since this narrowed 70 possible paths down to 2.
As I have said elsewhere, this problem is more of a puzzle than a math problem, so I'm interested in the variety of approaches to solving this. I really don't know what would be the best approach to take if I were to solve this problem myself.
I tried the same idea. It helped. I've never studied hyperbolic trig functions before- so this was a difficult problem. Ultimately, I got a bit lucky.
Note that tan ( cot − 1 x ) = x − 1 c o s e c h ( sinh − 1 x ) = x − 1 for nonzero real x . Thus tan ( cot − 1 ( c o s e c h ( sinh − 1 ( x ) ) ) ) = x for nonzero real x . We only now need to note that tanh ( c o s e c h − 1 ( x ) ) = x 2 + 1 s g n ( x ) cot ( sin − 1 ( x 2 + 1 s g n ( x ) ) ) = x for real nonzero x , so we see that the correct sequence is 1 2 7 1 2 1 3 1 4 1 9 2 4 2 5 making the answer 1 1 7 . The inverse trigonometric and inverse hyperbolic functions require careful argument choices to extend to the complex plane, but analytic continuation will be enough to show that tan ∘ cot − 1 ∘ c o s e c h ∘ sinh − 1 a n d cot ∘ sin − 1 ∘ tanh ∘ c o s e c h − 1 both act as the identity on C \ { 0 , i , − i } (and not just on the nonzero reals), which is what we want.
As always, an excellent solution. But this problem is more of a puzzle than a math problem, because there are 70 possible paths, and only one of them works. Even I'm not sure what's a systematic way of finding that one path that works, except through trial and error. Or look for pairs of pairs as you apparently have done. I provided the link to the Gudermannian Function site in hopes the reader would make use of the identities to look for the right path a little more efficiently.
And, yes, "careful argument choices to extend to the complex plane" was a problem for me in finding the right sequence of nested trigonometric functions, because much of the time it only works for a limited range of values for x , if at all.
I just chose a path which nests inverse function and the function or vice versa together.
The nesting of two is within same type i.e. trigonometric and hyperbolic. Pairing sequence is (1) arccsch, tanh, (2) arcsin, cot , (3) arcsinh, csch and (4) arccot, tan.
Testing with Wolfram Alpha gave positive result. Summing all the digits answer is 1+2+7+12+13+14+19+24+25=117
In fact, there are other nested series of functions possible that do not alternate between trigonometric functions and their inverses, but they yield an unchanged x only for some range of values.
Here is a Matlab / Octave code for solving this problem:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
|
Yes, this problem probablly should be in the "Computer Science" category.
Because each two functions like A r c C s c h & C s c h is just same as x × 1 which is x .
The path way number is 1 , 2 , 7 , 1 2 , 1 3 , 1 4 , 1 9 , 2 4 , 2 5
And the answer is 1 1 7
The 2nd pathway you've listed doens't work. If x = 0 . 5 , then you end up with 1 . 7 3 2 0 5 . . .
How to INCORRECTLY solve this problem: 1) find the highest possible value of your track:1+6+11+16+21+22+23+24+25=149 2) find the lowest possible value of your track: 1+2+3+4+5+10+15+20+25=85 3) find the average of these values: (149+85)/2=117
Probability says this value should be pretty close... and what do you know!
8 5 , 8 9 , 9 3 , 9 7 , 1 0 1 , 1 0 5 , 1 0 9 , 1 1 3 , 1 1 7 , 1 2 1 , 1 2 5 , 1 2 9 , 1 3 3 , 1 3 7 , 1 4 1 , 1 4 5 , 1 4 9 are all the possible sums there can be, and 1 1 7 is right in the middle. Picking 1 1 3 , 1 1 7 , 1 2 1 in 3 tries would have a probability 7 0 2 2 of winning.
The path is the nested function
T a n ( A r c C o t ( C s c h ( A r c S i n h ( C o t ( A r c S i n ( T a n h ( A r c C s c h ( x ) ) ) ) ) ) ) ) = x
so the following rooms are passed through
1 , 2 , 7 , 1 2 , 1 3 , 1 4 , 1 9 , 2 4 , 2 5
which totals 1 1 7
Let g d ( x ) be the Gudermannian Function . Then we have the following identities
1) S i n ( g d ( x ) ) = T a n h ( x )
2) C o t ( g d ( x ) ) = C s c h ( x )
3) T a n ( g d ( x ) ) = S i n h ( x )
From 1) and 2) we have
g d ( x ) = A r c S i n ( T a n h ( x ) )
C o t ( g d ( A r c C s c h ( x ) ) = x
C o t ( A r c S i n ( T a n h ( A r c C s c h ( x ) ) ) = x
From 3) and 2) we have
T a n ( g d ( A r c S i n h ( x ) ) = x
g d ( x ) = A r c C o t ( C s c h ( x ) )
T a n ( A r c C o t ( C s c h ( A r c S i n h ( x ) ) ) ) = x
Combining the two, we have
T a n ( A r c C o t ( C s c h ( A r c S i n h ( C o t ( A r c S i n ( T a n h ( A r c C s c h ( x ) ) ) ) ) ) ) = x
so if one starts out, for example, as x = 0 . 5 , one would go through the following values
0 . 5 , 1 . 4 4 3 6 4 , 0 . 8 9 4 4 2 7 , 1 . 1 0 7 1 5 , 0 . 5 , 0 . 4 8 1 2 1 2 , 2 . , 0 . 4 6 3 6 4 8 , 0 . 5
and escaping as 0 . 5 . The only values x cannot start with is i , − i , or 0 as that would leave you indeterminate.