Escape Satan And Save Mathematics!

Computer Science Level 3

This problem was inspired by this problem .

After having his demon henchmen thwarted by the cunning mathematician village chiefs of Earth,the devil himself comes down to Earth to get rid of the problem once and for all.

Confidently he snarls

" All you people of Earth stand in a large CIRCLE and number yourself starting from $1$ to $10^7$ . I will devour every $666th$ person and keep going around and around the circle eating up every $666th$ person and keep doing this till there is only $1$ person left. That last person I will spare and he is free to escape. "

You are the last living descendant of the mathematician village chiefs and need to ensure that you survive so that mathematics will not perish from Earth.

Which number will you choose to be the last person standing and escape the clutches of Satan ?

Details and assumptions

Assume all this happened a long time ago and that Earth only had $10^7$ inhabitants.
Satan will start eating from the $666$ th person.
This is an instance of a very famous problem called the Josephus Problem.

Example

It there were $9$ people and every $5$ th person was eaten the people eaten would be $5\rightarrow 1\rightarrow 7\rightarrow 4\rightarrow 3\rightarrow 6\rightarrow 9\rightarrow 2$ leaving the $8$ th person alive.

The answer is 9337541.

3 solutions

Eric Zhang
Apr 21, 2014

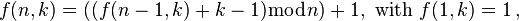
Python 2 solution (takes a few seconds but too long):

def josephus(n, k):
    r = 0
    i = 1
    while i <= n:
        r = (r + k) % i;
        i += 1
    return r + 1

print josephus(10 ** 7, 666)

I didn't use recursion because max. recursion depth is exceeded.

I wrote some code in C# for the test case in the problem (1 to 9) and arrived at the foll code -

        ArrayList ar = new ArrayList();
        ArrayList arn = new ArrayList();
        int nn = 0;

        for (int i = 1; i <= 9; i++)
        {
            ar.Add(i);
        }

    F1: int kk = nn + 4;

        Application.DoEvents();
        lblCounter.Text = ar.Count.ToString();

        if (ar.Count.Equals(1))
        {
            MessageBox.Show("Answer is : " + ar[0].ToString());
            return;
        }

        try
        {
            if (kk > ar.Count) kk = kk - (ar.Count);
            MessageBox.Show(ar[kk].ToString());
            ar.RemoveAt(kk);
        }
        catch
        {

        }

        kk += 5;

        if (kk > ar.Count)
        {
            kk = kk % (ar.Count + 1);

        }
        if (kk.Equals(ar.Count))
        {
            kk = ar.Count - 1;
        }
        MessageBox.Show(ar[kk].ToString());
        ar.RemoveAt(kk);
        nn = kk;

        arn.Clear();

        for (int h = 0; h < ar.Count; h++)
        {
            arn.Add(ar[h]);
        }

        ar.Clear();

        for (int y = 0; y < arn.Count; y++)
        {
            ar.Add(arn[y]);
        }

        goto F1;
    }

The numbers are identical upto the last iteration but my answer is 2 (not 8). If someone understands C# can somebody pls guide me as to whats wrong?

Sanjay kamath - 7 years, 1 month ago

That's why I prefer C over python sometimes (basically where it comes to computational case). But in the 5th line why the semicolon? :p (It's not pythonic)

Sudip Maji - 6 years, 10 months ago

Could you please explain why it works?

Ajay Kumar - 5 years, 9 months ago

Wow - I did it the hard way and it took all day - your solution took 2 seconds tops....

Terry Smith - 4 years, 8 months ago

Thaddeus Abiy
Apr 17, 2014

In C++ ~0.02seconds

// This is the classic Josephus problem

#include <iostream<iostream>>
int main()
{
    int r = 0;
    int i = 1;
    int n  = 10000000;
    int k = 666;
    while (i <= n){
        r = (r + k ) % i;
        i += 1;
    }
  std::cout << r + 1 << std::endl;
  return 0;
}

The mathematics behind this for the "every other person" is well understood in the Josepheus problem . What would be the mathematical solution to this version?

Calvin Lin Staff - 7 years, 1 month ago

As from the Wikipedia page,the general case can be expressed in a recurrence relation : $ddd$ ddd

Thaddeus Abiy - 7 years, 1 month ago

I got a time limit error :(

Tan Li Xuan - 7 years, 1 month ago

Sorry, I forgot how slow python was sometimes..I ported the same solution to C++.It runs significantly faster now.

Thaddeus Abiy - 7 years, 1 month ago

I did the same code in python(I didn't know how to use C++)

Tan Li Xuan - 7 years, 1 month ago

Nikunj Lahoti
May 1, 2014

/* 
Idea is to actually create the population and rejoice the killing :D 
This solution is far from performant. //Takes around 5 minutes to execute.
*/

//Time taken to create the LinkedList: 39780 ms
//Time taken to kill everyone but one: 277618 ms


public class JosephusProblem {

    public static final int N = 10000000;
    public static final int K = 666;

    public static void main(String[] args) {
        new JosephusProblem().go();
    }

    private void go() {
        long startTime = System.currentTimeMillis();
        Node<Integer> parent = getCircularList();
        long endTime = System.currentTimeMillis();
        System.out.format("Time taken to create the LinkedList: %d ms%n", endTime - startTime);

        //Pass on the circular linked list
        long anotherStartTime = System.currentTimeMillis();
        System.out.format("Please stand on the %d position if you want to live!%n", eliminate(parent));
        long anotherEndTime = System.currentTimeMillis();
        System.out.format("Time taken to kill everyone but one: %d ms%n", anotherEndTime - anotherStartTime);
    }

    private Node<Integer> getCircularList() {
        Node<Integer> root = new Node<>(1);
        Node<Integer> current = root;
        for (int i = 2; i <= N; i++) {
            current.next = new Node(i);
            current = current.next;
        }
        current.next = root;
        Node<Integer> parent = new Node<>(0);

        parent.next = root;
        return parent;
    }

    private int eliminate(Node<Integer> node) {
        int size = N;
        while (node.next != node) {
            for(int i = 1; i < K; i++) {
                node = node.next;
            }
            node.next = node.next.next;
            size--;
            //if (size % 10000 == 0) System.out.println(size);
        }
        return node.value;
    }

}

class Node <T> {
    T value;
    Node<T> next;

    public Node(T value) {
        this.value = value;
    }
}

1	`Actual killing will be done by the GC :)`

Nikunj Lahoti - 7 years, 1 month ago

Escape Satan And Save Mathematics!

The answer is 9337541.

3 solutions

0 pending reports