Escape The Even Demon

Number Theory Level 2

You are the village chief. Your village has 1000 residents including yourself. One day the ferocious EVEN DEMON attacks your village and snarls,

"All you 1000 villagers stand in a large CIRCLE, numbering yourself from 1 to 1000. Starting from number 1, I will eat every second villager (which means he will eat villager number 2, then villager number 4 and so on) and keep going around and around the circle eating up every second villager and keep doing this till there is only 1 villager left. That last villager I will spare and he is free to escape."

Since you are the village chief, you have the right to choose where you wish to stand.

In the original circle of 1000 villagers which number will you choose to stand at to be the last villager standing and escape the clutches of the EVEN DEMON?

This problem is not an original. It is adapted from a famous problem recorded by a Jewish historian.

The answer is 977.

8 solutions

Satyen Nabar
Apr 7, 2014

When the number of participants is a power of two :

Regardless of the number of participants n, person 1 survives the first pass. Since n is even, as every positive power of two is, person 1 survives the second pass as well. In the first pass, the process goes like this: person 1 is skipped, person 2 is eliminated, person 3 is skipped, person 4 is eliminated, … , person n-1 is skipped, person n is eliminated. The second pass starts by skipping person 1.

As long as the number of participants per pass is even, as it will be for a power of two starting point, the same pattern is followed: person 1 is skipped each time. Therefore, for any power of two, person 1 always wins.

When the number of participants is not a power of two, we know this much: person 1 can’t be the winner. This is because at least one pass will have an odd number of participants. Once the first odd participant pass is complete, person 1 will be eliminated at the start of the next pass.

Powers of two come into play here, but you have to change your perspective to see them. They don’t occur on pass boundaries — they span them. At some point, during pass 1, the number of participants remaining becomes a power of two. For example if there are 13 villagers, that occurs when 5 of the 13 people are eliminated, leaving an 8 person problem: 11, 12, 13, 1, 3, 5, 7, 9. This means person 11, the first person in the new power of two circle, wins.

Write n as n = 2^m + k, where 2^m is the largest power of two less than or equal to n. k people need to be eliminated to reduce the problem to a power of two, which means 2k people must be passed over. The next person in the circle, person 2k + 1, will be the winner. In other words, the winner w is w = 2k + 1.

n=1000. k=1000- 512 (largest power of 2 below 1000) = 488. w = 2k+1 = 977.

So nice!

Richard Polak - 7 years, 1 month ago

your question says that he will start at number 1 and eat every second person. dose this mean he will look at person 1 and eat the man next to him or eat person 1 first

keanu duPont - 6 years, 5 months ago

Can you generalize it for $n$ people?

Akshat Sharda - 5 years, 2 months ago

Note that this is actually the Josephus Problem

This can easily be solved by this algorithm without a proof:

1.) Turn the number $n$ into binary (e.g. $1000 = 1111101000_2$ )

2.) Transfer the leading digit to the rightmost of your new number (e.g. $1111101000_2 \rightarrow 1111010001_2$ )

3.) Turn your number formed in step two back to decimal (e.g. $111101000_2 = 977$

Viola!!!

Hans Gabriel Daduya - 3 years, 4 months ago

That’s equivalent to the answer above: When satyen took out the highest power of 2, that’s equivalent to taking out the 1 in the left in binary representation, Then when he multiplied by 2 and added 1, that’s multiplying by 10 and add one in binary, ie add 1 in the right. So that looks like a rotation where you take out the one from the left and add it to the right :)

Omar Rekhis - 2 years, 7 months ago

Very nice explanation.

William Downing - 2 years, 8 months ago

I used the same process.............!!!!!

Aman Bansal - 7 years, 2 months ago

Nice explanation, did same process

Mardokay Mosazghi - 7 years, 2 months ago

I solved it the same way...

Eddie The Head - 7 years, 2 months ago

Nice !!!

Sourabh Mane - 7 years, 2 months ago

good question

BHANU VISHWAKARMA - 7 years, 2 months ago

thanks . that explanation helps me a lot .

Nirob 3.1416 - 7 years, 2 months ago

Great solutiuon and great way of explaining it too

Souradeep Roy Choudhury - 7 years, 1 month ago

Prerna Kashyap
Jul 7, 2014

//This method is unconventional, but it works like a charm.
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;

void delete_ele(int pos, int input[], int *len)
{
    int i;
    for(i=pos;i<*len;i++)
        input[i]=input[i+1];
    (*len)--;
}

int main()
{
    int input[1000], i, len;
    len=1000;
    for(i=0;i<len;i++)
        input[i]=i+1;
    i=-1;
    while(len>1)
    {
        i+=2;
        if(i>=len)
        {
            while(i>=len)
                i=i-len;
        }
        delete_ele(i, input, &len);
        i--;
    }
    cout<<input[0];
    return 0;
}

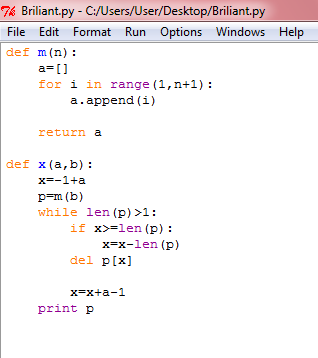
Nice. Using code. Did the same.

Muhammad Reza - 4 years, 5 months ago

Shi Zhz
Apr 24, 2014

I admire people who can see the answer in the math way, I found it by a program:

def survivor(n):
    """produce the survivor position in the circle of number n"""
    circle = range(1, n + 1)
    eat_from = 1
    last_in_circle = circle[-1]
    while len(circle) > 1:
        circle = filter(lambda (i, x): (i - eat_from) % 2 != 0, enumerate(circle))
        circle = map(lambda x: x[1], circle)
        eat_from = last_in_circle != circle[-1] + 0 # if the last person in the circle is eaten, then eat from the second position next time, otherwise, eat from the first position next time
        last_in_circle = circle[-1]

    return circle

print survivor(1000)

Masbahul Islam
Dec 10, 2015

Charlz Charlizard
Jul 8, 2015

Generalization of this is Tn=1-N+2K..Where n=Uneaten No. or Safe number.... N=2^m..m=f(g(log k/log2)...where g(x)=antilog of x..f(x)=ceiling function of x..K=No. of people standing in the circle..

So in our case k=1000 so N=1024...Tn=1-1024+2000=977..

Aryan Gaikwad
Apr 3, 2015

public static void main(String args[]){
    System.out.println(josh(1000, 2));
}

private static int josh(int m, int n){
    List<Integer> list = new ArrayList<Integer>();
    for(int i = 1; i <= m; i++)
        list.add(i);
    int i = n;
    while(list.size() != 1){
        int len = list.size(), rem = 1;
        for(; i <= len; i += n)
            list.remove(i - rem++);
        i = n - (len - (i - n));
        rem = 1;
    }
    return list.get(0);
}

It takes about 0.001 second to run

Sri Balusu
Oct 11, 2014

If 2^k ≤ n < 2^k+1 then f(n)=2(n−2^k)+1. Therefore, 2^9 ≤ 1000 < 2^10, implies f(1000) = 2(1000 - 2^9) + 1 i.e , f(1000) = 2*488 + 1 = 977.

Agnishom Chattopadhyay
Apr 24, 2014

http://rosettacode.org/wiki/Josephus_problem#Mathematica

It is so powerful and elegant that it hurts.

Bernardo Sulzbach - 6 years, 11 months ago

Escape The Even Demon

The answer is 977.

8 solutions

0 pending reports