ET arrives at an alien angle

Let $'v'$ be the velocity of the package when it grazes the surface of earth.

Since the origin of the frame is located at the center of earth, for the system $'spaceship + package'$ , the external torque is 0 because the forces acting on it are radial. So the angular momentum is conserved. Furthermore, the final velocity vector of the package has to be perpendicular to the position vector, otherwise the instrument package would crash on earth , so: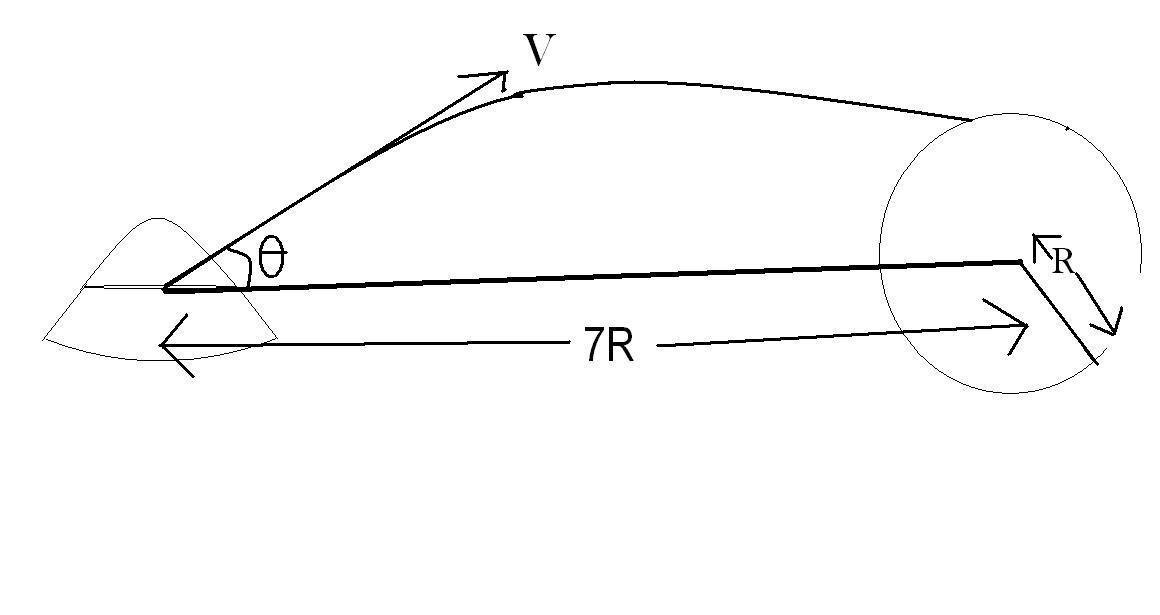

$L_{initial}$ = $L_{final}$ , where $L$ is the angular momentum of the defined system.

=> $7mv_{0}R\sin(\theta$ ) = $mvR\sin90$

=> $7v_{0}\sin(\theta$ )= $v$ ....... $(i)$

Now, by conserving energy, we get: $\frac{mv_{0}^2}{2} - \frac{GMm}{7R} = \frac{mv^2}{2} - \frac{GMm}{R}$ => $v^2-v_{0}^2 = \frac{12GM}{7R}$ .... $(ii)$

Now, Squaring $Eq(i)$ , rearranging and replacing in $Eq(ii)$ , we get: $v_{0}^2( 49\sin^{2}(\theta) -1) = \frac{12GM}{7R}$

THEREFORE , $\sin(\theta) = \frac{1}{7}\sqrt {1+\frac{12GM}{7v_{0}^2R}}$

Plugging in the values, we get: $(\theta) = {\sin^{-1}(\frac {\sqrt {1.742}}{7})}$

THEREFORE, $p+q = 8.742:)$