Euclidea-Style Time!

Geometry Level 1

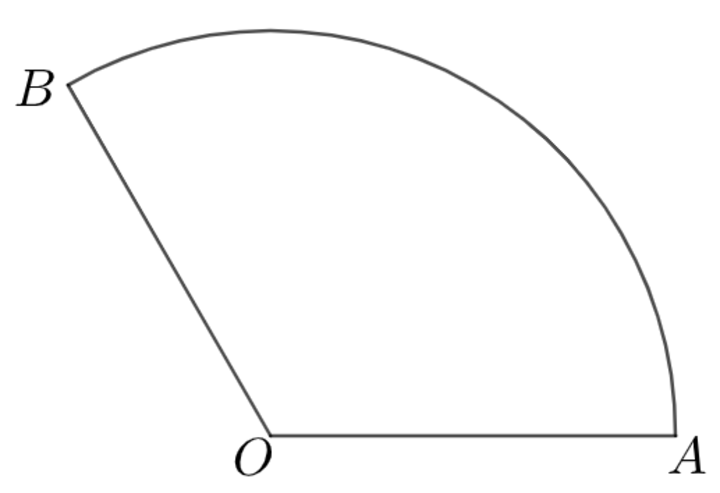
Given the circular sector $BOA$ , where $O$ is its center, can we divide it into two parts of even area, using only the compass and the ruler?

Note: This problem is inspired by Euclidea , the geometric construction game involving the straightedge and the compass.

Yes No

2 solutions

Tom Engelsman
Jan 22, 2021

With the compass, draw two circular arcs (one centered at $A$ , the other at $B$ ) with respectively equal radii $AO, BO$ . Call the second intersection point of these two arcs $X$ which coincides with the midpoint of arc $AB$ . With the ruler, draw the line $OX$ such that radius $OX$ is the bisector of $\angle{AOB}$ , thus dividing our original sector into two regions of equal area.

Answer = $\boxed{YES}.$

It is technically an angle bisector

Durvish Suresh - 4 months, 1 week ago

@tom engelsman - Hi Tom! Nice solution. One note: point $X$ does not necessarily coincide with the midpoint of arc AB. This happens when $\angle AOB=120{}^\circ$ .

Thanos Petropoulos - 3 months ago

Steven Adler
May 31, 2021

One can always bisect an angle using compass and straightedge. Make congruent arbitrary line segments on OA and OB. Call these segments OX and OY. Connect X and Y with the straightedge. Find the perpendicular bisector of XY. It will pass through O, bisecting angle AOB. It will also pass through arc AB, dividing sector AOB into two congruent parts.

Euclidea-Style Time!

2 solutions

0 pending reports