Reducing The Exposure

Let $\angle CAD = P, \angle EAD = Q$ , then $\cot(\angle CAE) = \cot(\alpha) = \cot(P-Q)$ .

Let $AD = k$ , then $DF=FE+EC=AD = k$ .

So, $\tan( P) = \dfrac{DC}{AD} = \dfrac{k+k+k}{k} = 3$ , and $\tan (Q) = \dfrac{DE}{AD} = \dfrac{k + k}{k} = 2$ .

Using the difference formula ,, $\tan(P-Q) = \dfrac{\tan P - \tan Q}{1+ \tan P \tan Q} = \dfrac{3 - 2}{1 + 3 \cdot 2} = \dfrac17$ .

Hence, $\cot(P - Q) = \dfrac1{\tan (P-Q)} = \boxed 7$ .

Assume without loss of generality $AD$ is 1. Then $DC$ is 3, and $EC$ is 1. Note this implies by the Pythagorean Thorem $EQ = \sqrt{1^2 + 3^2} = \sqrt{10} .$

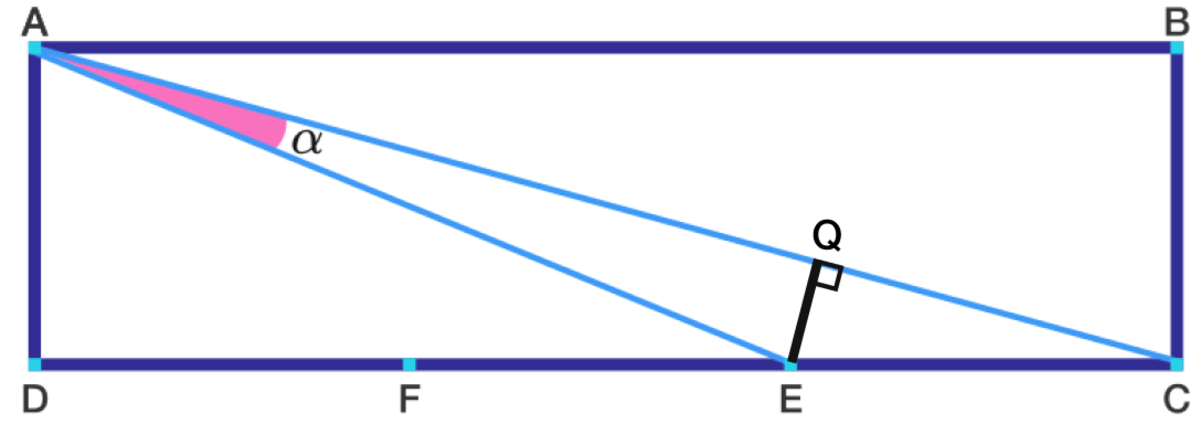
Drop a perpendicular from $E$ to $AC,$ and call new point $Q.$ $\triangle ADC \sim \triangle EQC$ by AA similarity. This implies the ratio $EQ/AD = EC/AC .$ Substituting values, $EQ = 1/\sqrt{10} .$

Since $\triangle ADG \sim \triangle EQG ,$ $QC$ is $3EQ$ so $QC = 3/\sqrt{10} .$

By subtraction, $AQ = AC - QC = \sqrt{10} - 3\sqrt{10} = 7/\sqrt{10} .$

Thus the cotangent of $\angle CAE$ is $\frac{AQ}{EQ} = \frac{7/\sqrt{10}}{1/\sqrt{10}} = 7 .$

Using Sine Rule (Law of Sines) we know that $\dfrac{\sin(\angle CAE)}{EC} = \dfrac{\sin(\angle ECA)}{AE}$ .

Now, using the definition of sine and the Pythagorean theorem , we get that $\dfrac{\sin(\angle CAE)}{EC} = \dfrac{\sin(\angle ECA)}{\sqrt{5EC^2}} \Rightarrow \sin(\angle CAE) = \dfrac{\sin(\angle ECA)}{\sqrt5}$ .

Again using the definition of sine, we get that $\sin(\angle ACE) = \dfrac{AD}{AC} = \dfrac1{\sqrt{10}} \Rightarrow \sin(\angle CAE) = \dfrac1{\sqrt{50}}$ .

Now using the fact that $\cot x = \dfrac{\cos x}{\sin x}$ and the fact that $\cos x= \sqrt{1 - \sin^2x}$ , we get $\cot(\angle CAE) = \boxed{7}$ .

• Thinking of $A$ as the origin of a cartesian plane, we have $E=\left( 4,-2 \right)$ and $C=\left( 6,-2 \right)$ .
• Let $\vec { AE } =4\hat { \imath } - 2\hat { \jmath }$ and $\vec { AC } =6\hat { \imath } -2\hat { \jmath }$ .
• Using the equality from the dot product* of them it develops to $\left| \vec { AE } \right| \cdot \left| \vec { AC } \right| \cos { \alpha } =6\cdot 4+\left( -2\cdot -2 \right)$ .
• Calculating the moduli of the both vectors is simple and then we have $\sqrt {20} \cdot \sqrt {40} \cos { \alpha } = 28 \implies \cos{ \alpha }=\frac { 7\sqrt { 2 } }{ 10 }$ .
• By Trigonometry we know that $\frac {1}{\cos {x} } = \tan ^{ 2 }{ x } + 1$ , which ultimately leads to $\cos ^{ { 2 } }{ \alpha } =\frac { 49\cdot 2 }{ 100 } \implies \cos ^{ { 2 } }{ \alpha } -1=\dfrac { 49\cdot 2 }{ 100 } -1 = \tan ^ {2} { \alpha } \implies \tan {\alpha } = \frac {1}{7}$

• $\tan { \alpha } = \frac {1}{\cot { \alpha }} \implies \boxed {\cot {\alpha } = 7}$

• * Dot Product from two vectors

Let ${\bf x = AD, }$ from the given information it follows that ${\bf AB = 3x, EC = x, DE = 2x \implies }$ $$

${\bf AC = \sqrt{10} x, AE = \sqrt{5} x }$ $$

The law of cosines ${\bf \implies 1 = 15 - 10\sqrt{2}cos\alpha \implies cos\alpha = \frac{7}{5\sqrt{2}} }$ $$

${\bf \implies cot\alpha = 7. }$