Euler Euler?
The Bătinețu's sequence { b n } n ≥ 2 is defined as b n = n + 1 ( n + 1 ) ! ( n + 1 ) 2 − n n ! n 2 . Find
n → ∞ lim ( 1 + n b n ) n n − 2 1 ∑ k = 0 n k + 1 n k ( k n )
This problem, taken from Romanian Mathematical Magazine , was proposed by teacher Florică Anastase, Romania .
The answer is 1618.177.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
b n is a sequence which tends to e as n → ∞ . We can use Stirling's Approximation
as b n → l i m n → ∞ e ( n + 1 ) − n e = e
So ( 1 + n b n ) can be approximated quite well to 1 + n e as n → ∞ .
Next for ∑ r = 0 n r + 1 n r ( r n ) = n ( n + 1 ) n − ( n + 1 ) ( n ) 1
You can use integration of ( 1 + x ) n from 0 to n and the well known identity of binomial theorem to prove this . Or you can use basic rearrangement of the series. This is a well known result...hence I am not proving this.
So a good approximation for this limit would be:-
lim n → ∞ ( 1 + n e ) n n − 2 1 ( n ( n + 1 ) n − ( n + 1 ) ( n ) 1 )
So now using the formula for 1 ∞ form of limits we have our approximation as :-
e lim n → ∞ ( n e n n n 2 ( n n + 1 n − ( n + 1 ) ( n ) 1 )
e lim n → ∞ ( n e ( n 2 ) ( n ( 1 + n 1 ) n − ( n n ) ( n + 1 ) ( n ) 1 )
Using the fact that ( 1 + n 1 ) n tends to e and n 2 1 ( n n ( n + 1 ) 1 ) tends to 0 as n → ∞ we have another approximation as :-
our limit is approximated to
e lim n → ∞ n 2 e ⋅ e ⋅ n 2
= e e ⋅ e
e e 2 .
now as for the approximations I do not have any formal proofs for those approximations....but I post the pictures of the graphs....perhaps someone more skilled than me at real analysis could prove these.
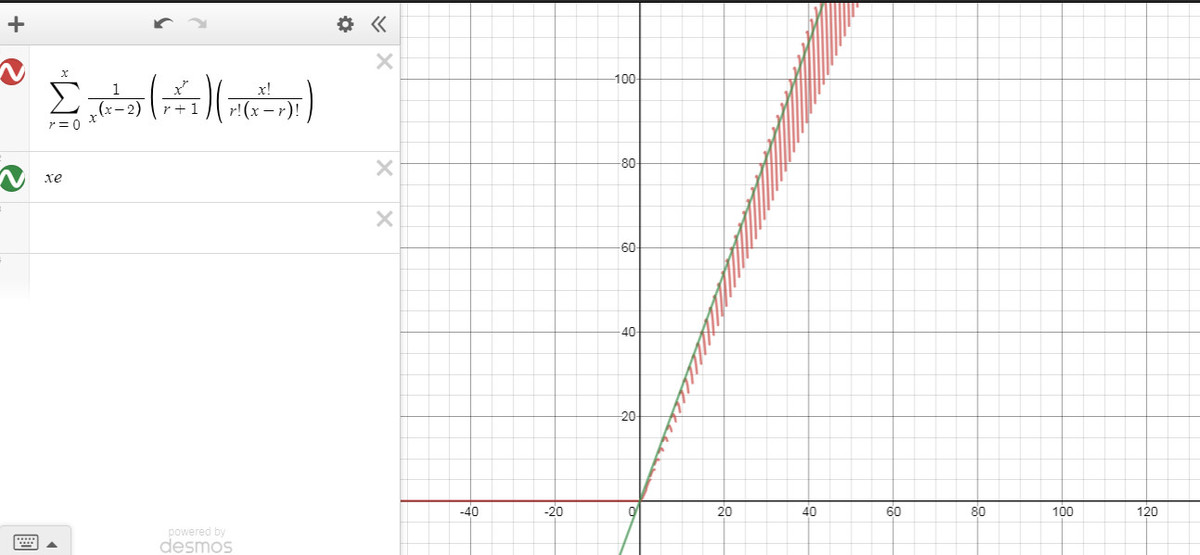
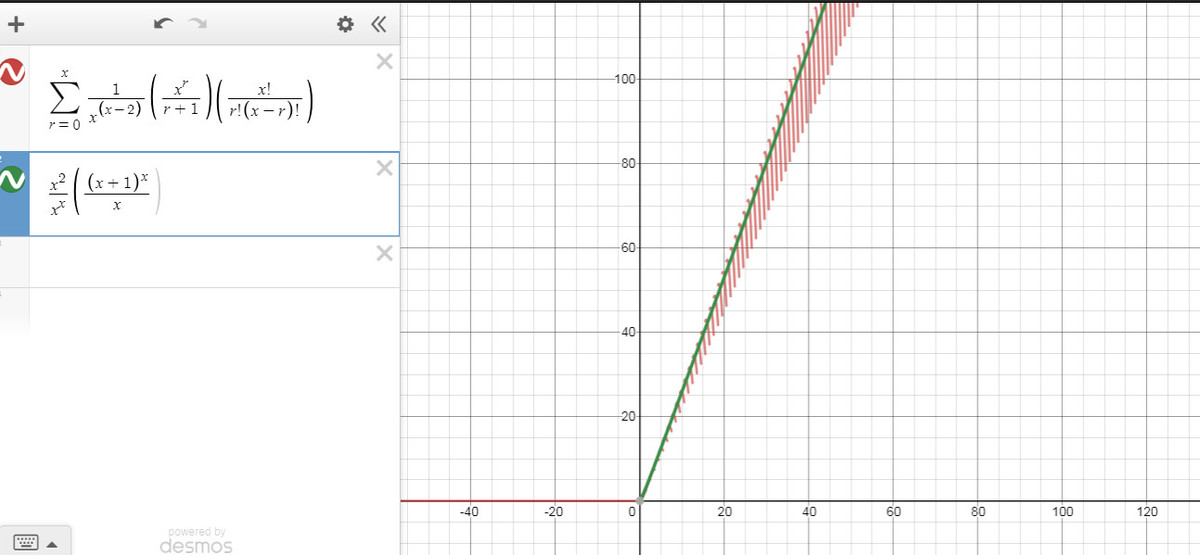
 and hence
Ω
=
e
e
2
≈
1
6
1
8
.
1
7
7
.
and hence
Ω
=
e
e
2
≈
1
6
1
8
.
1
7
7
.