Problem of Sylvester

If we write $\mathbf{a} = \overrightarrow{OA}$ , $\mathbf{b} = \overrightarrow{OB}$ , $\mathbf{c} = \overrightarrow{OC}$ , then $|\mathbf{a}| \; = \; |\mathbf{b}| \; = \; |\mathbf{c}| \; = \; R$ where $R$ is the outradius, and hence $(\mathbf{a}-\mathbf{b})\cdot(\mathbf{a}+\mathbf{b}) \; = \; |\mathbf{a}|^2 - |\mathbf{b}|^2 \; = \; 0$ Thus $\mathbf{a}+\mathbf{b}$ is perpendicular to $\overrightarrow{AB}$ , and hence the altitude through $C$ has equation $\mathbf{r} \; = \; \mathbf{c} + \lambda(\mathbf{a} + \mathbf{b}) \hspace{2cm} \lambda \in \mathbb{R}$ Thus the altitude passes through the point with position vector $\mathbf{a}+\mathbf{b}+\mathbf{c}$ . By symmetry, this is true for all the other altitudes, and hence we have identified the orthocentre $\overrightarrow{OH} \; = \; \mathbf{a} + \mathbf{b} + \mathbf{c}$ making the answer $m = \boxed{1}$ .

We know if the centroid of the triangle $\Delta ABC$ is $G$ , then $\overrightarrow{OH} = 3\overrightarrow {OG}$ . Now we know that $\overrightarrow{OG}=\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$ . Combining these we get $m=\frac{3}{3}=1$ .

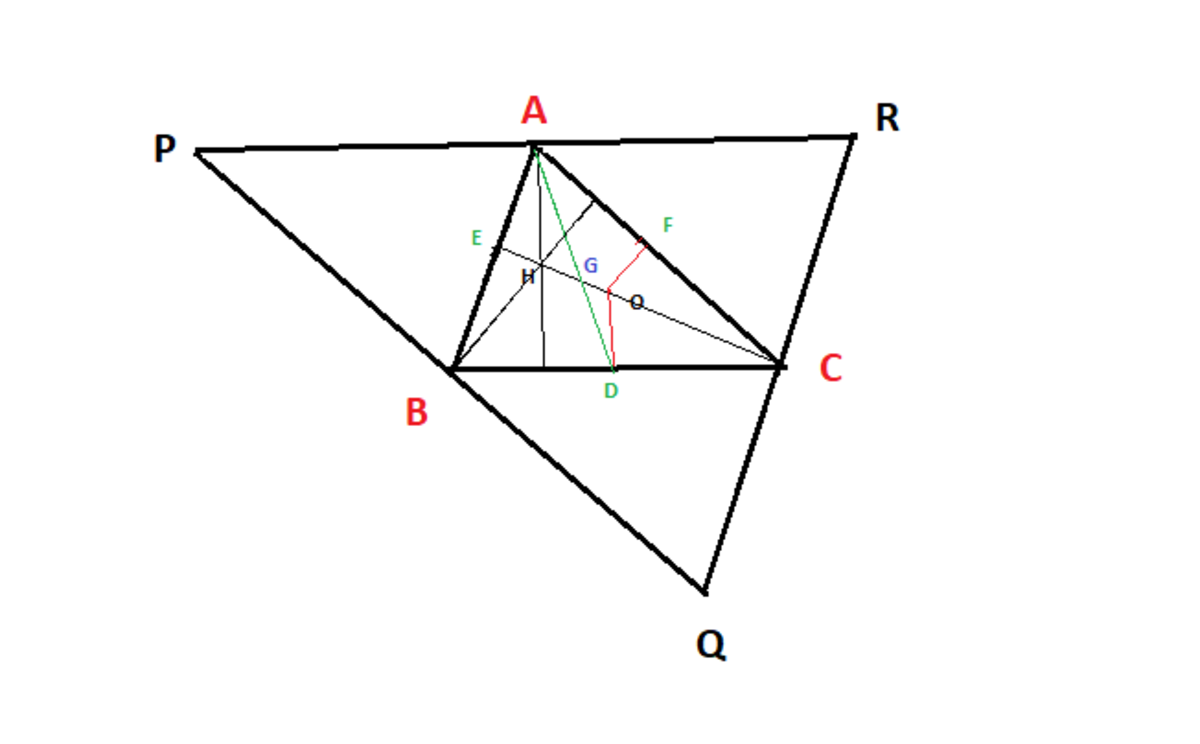
In this $\Delta ABC$ the points $H,O,G$ are the Orthocenter, Circumcenter and Centroid respectively. Draw $\Delta PQR$ .Let it be the tringle twice of $\Delta ABC$ and inverted such that $AB||QR ; AC||PQ$ and $BC||PR$ . And $PA=AR ; PB=BQ ; QC=CR$ . Thus, $H$ becomes the circumcenter of $\Delta PQR$ as well as the orthocenter of $\Delta ABC$ . From the symmetry we can conclude that $AH=2DO$ .

Let, the line $AD$ intersects $OH$ at $G$ . As, $AH||OD$ and $AH=2DO$ , we can say from the two symmetric triangles $\Delta AHG$ and $\Delta OGD$ that $AG=2GD$ . So, $G$ divides the line $AD$ in $2:1$ ratio and $D$ is the mid point of $BC$ . So, its certain that $G$ is the centroid of $\Delta ABC$ , $G$ lies on the line $OH$ and also $HG=2GO$ .So, $\overrightarrow {OH}=3\overrightarrow{OG}$ .