Euler might have known...
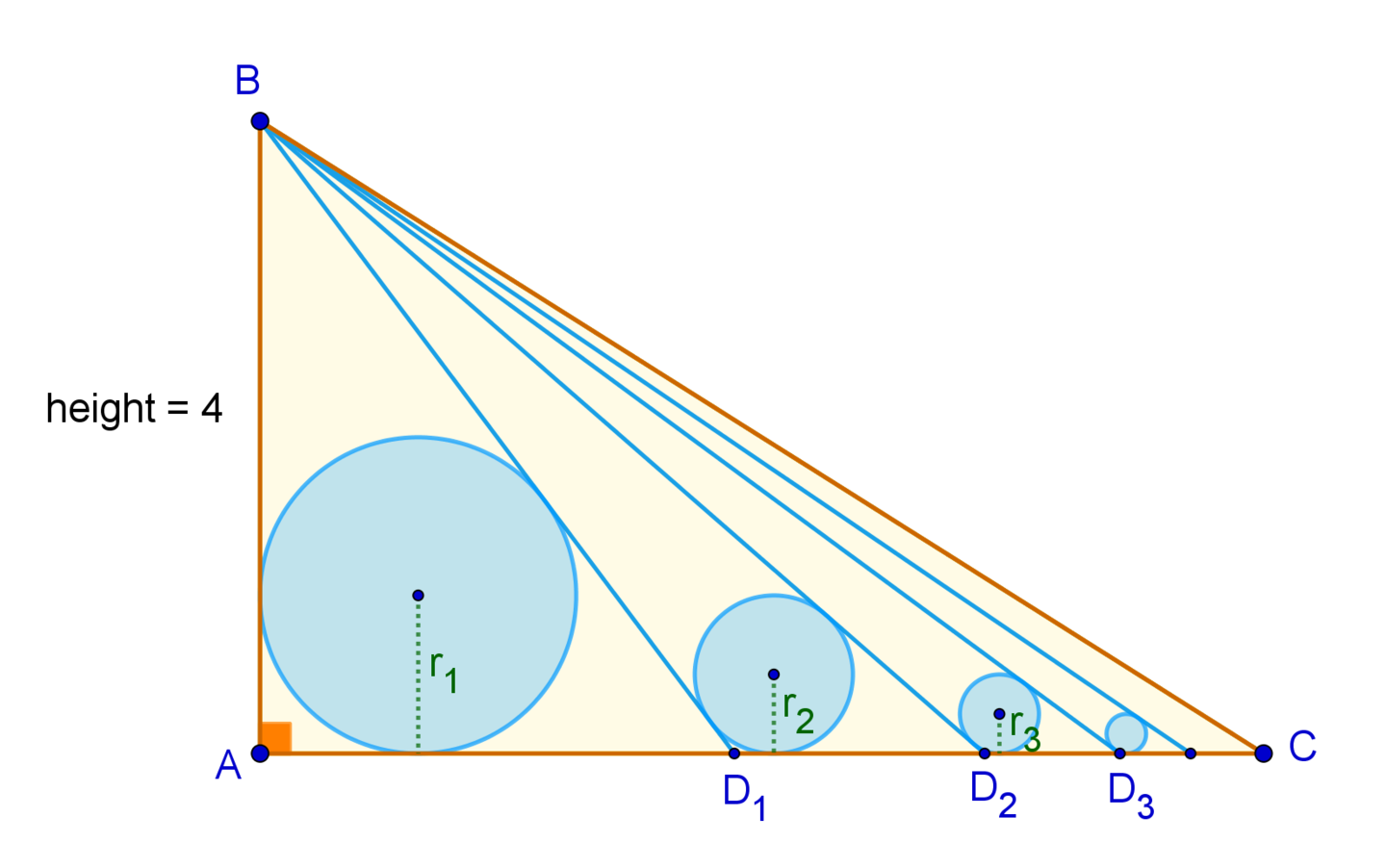
is a right triangle of height , partitioned into an infinite number of adjacent triangles by cevians , as seen in the figure. Inside every triangle , an incircle is inscribed with radius . The sequence is a geometric progression with and .
If is the area of , submit .
The answer is 12695834.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From this we can deduce that sec β = 4 ( 2 − r ) 1 [ r ( 4 − r ) tan α + ( r 2 − 4 r + 8 ) sec α ] and hence we have tan β + sec β cot ( 2 1 π − β ) + csc ( 2 1 π − β ) cot ( 4 1 π − 2 1 β ) tan ( 4 1 π − 2 1 β ) = 2 − r 2 ( tan α + sec α ) = 2 − r 2 [ cot ( 2 1 π − α ) + csc ( 2 1 π − α ) ] = 2 − r 2 cot ( 4 1 π − 2 1 α ) = ( 1 − 2 1 r ) tan ( 4 1 π − 2 1 α ) If we define θ n = ∠ A B D n to be the angle at the top of the triangle A B D n , we deduce that tan ( 4 1 π − 2 1 θ n ) = ( 1 − 2 1 r n ) tan ( 4 1 π − 2 1 θ n − 1 ) for any n ≥ 2 . If θ ∞ = ∠ A B C is the angle at the top vertex of the limiting triangle A B C , it follows from this that tan ( 4 1 π − 2 1 θ ∞ ) = tan ( 4 1 π − 2 1 θ 1 ) × n = 2 ∏ ∞ ( 1 − 2 1 r n ) Now tan θ 1 = 4 3 , so that tan 2 1 θ 1 = 3 1 , and hence tan ( 4 1 π − 2 1 θ 1 ) = 2 1 . Thus we deduce that tan ( 4 1 π − 2 1 θ ∞ ) = n = 1 ∏ ∞ ( 1 − 2 − n ) = ( 2 1 ; 2 1 ) ∞ where ( 2 1 , 2 1 ) ∞ is the q -Pochhammer symbol. Thus we deduce that tan ( 2 1 θ ∞ ) tan θ ∞ = 1 + ( 2 1 ; 2 1 ) ∞ 1 − ( 2 1 ; 2 1 ) ∞ = 2 1 ( ( 2 1 ; 2 1 ) ∞ 1 − ( 2 1 ; 2 1 ) ∞ ) and so the area of the triangle A B C is Δ = 8 tan θ ∞ = 4 ( ( 2 1 ; 2 1 ) ∞ 1 − ( 2 1 ; 2 1 ) ∞ ) = 1 2 . 6 9 5 8 3 4 0 9 7 4 7 3 8 . . . and hence ⌊ 1 0 6 Δ ⌋ = 1 2 6 9 5 8 3 4 .