Euler's count of circle pieces
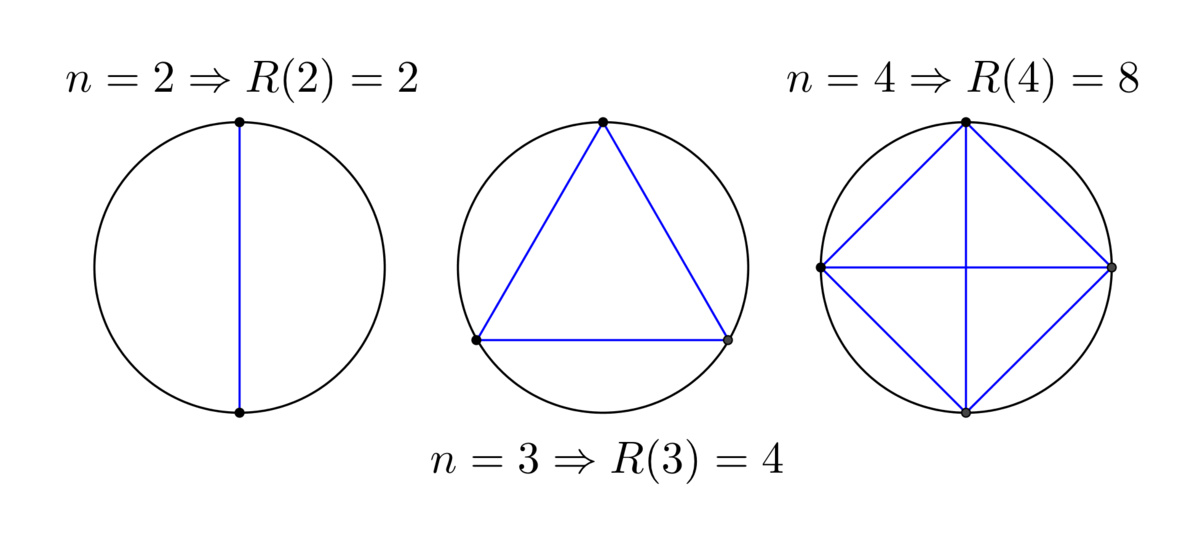
The function R ( n ) denotes the maximum number of areas which can be formed within the circle when all chords between n distinct points on a circle are drawn.
In the figures above we see that R ( 2 ) = 2 , R ( 3 ) = 4 and R ( 4 ) = 8 .
Find the smallest value of R ( n ) ≥ 1 0 0 0 .
Note: The n points lie on the circle in such a way that the 'maximum' number of areas are formed.
The answer is 1093.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Great job Otto! Good to read you liked working on the problem. Thank you for your excellent approach in using Euler's formula F = 2 − V + E . Your explanation is very clear and thorough.
When you state that E = n + ( 4 n ) you probably mean V = n + ( 4 n ) .
When substituting V and E in Euler's formula we can deduce an interesting alternative expression for F without the use of the given points.
The result is: F = 1 + ( 2 n ) + ( 4 n ) .
A somewhat educated guess (although a bit unnecessary I admit) for the desired value of n that I used was: n ≈ 4 4 ! × 1 0 0 0 + 1 . 5 ≈ 1 3 . 9 . A verification for n = 1 3 and n = 1 4 was sufficient.
Additional relevant question to other Brilliant-users: How can the alternative expression for F = 1 + ( 2 n ) + ( 4 n ) be deduced?
Interesting problem! Thanks for sharing!
Just a quick outline of my solution: Let V, E, and F be the number of vertices, edges, and faces we get if we place n points on the circle, "in general position".
We find V = n + ( 4 n ) : we have the n vertices on the circle, and for every four points on the circle we get a point of intersection as we draw two lines across.
Now every interior point has order 4, while the ones on the circle have order n + 1 , including the arcs of the circle in the count. Since every edge is counted twice this way, we find E = 2 n ( n + 1 ) + 2 ( 4 n ) .
Now we can use Euler's formula F = 2 − V + E − 1 to find the number of regions; we subtract 1 since we are told to count the regions inside the circle only. F will be a quartic polynomial in n; fitting it to the points you give us, (0,1), (1,1), (2,2), (3,4), and (4,8) we find F = 1 + 2 4 1 n ( n − 1 ) ( n 2 − 5 n + 1 8 ) . For n =14 we find F = 1 0 9 3 .