Eulers Egg, Random Numbers and Integration
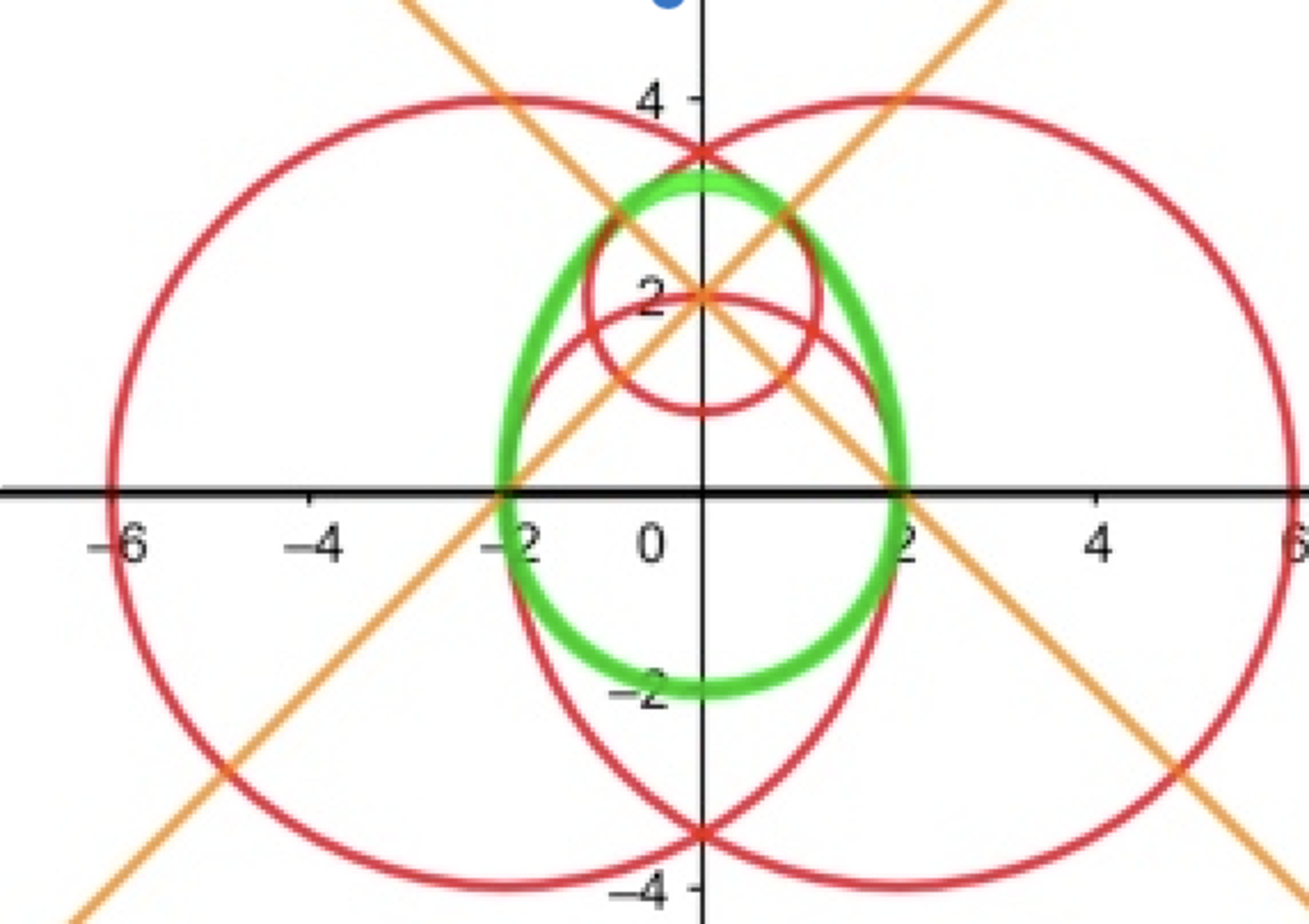
Given the above graph calculate the area within the Eggs green boundary using the Monte Carlo integration technique. Utilize a graphics package such as GeoGebra to aid in your solution.
The answer is 15.927.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Went for a similar geometrical solution. I've seen this as a variant on tangrams called the "egg of Columbus" - here , for instance.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
|
Below is my parallel C++ code. I have found the radius of the smallest red circle in a way similar to the one described by @Alak Bhattacharya . I use the symmetry: the experiment takes place only for the positive x coordinated.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 |
|
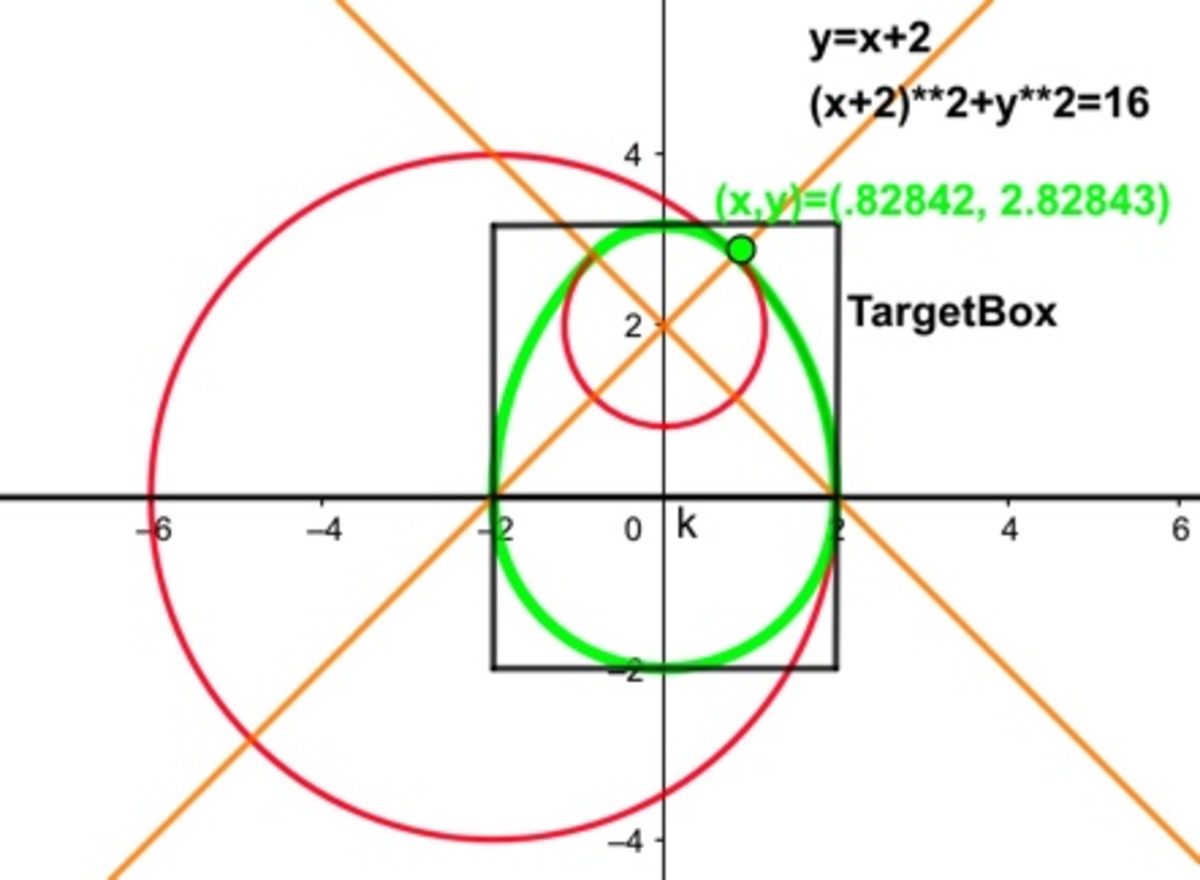
The yellow line ( y = x + 2 ) intersects the circle ( x + 2 ) 2 + y 2 = 1 6 at ( 2 √ 2 − 2 , 2 √ 2 ). Therefore the radius of the smallest red circle, r , is given by r 2 = 2 ( 2 √ 2 − 2 ) 2 = 8 ( 3 − 2 √ 2 ) . Area of the region within the egg is twice the sum of three areas : A 1 = 8 π r 2 = π ( 3 − 2 √ 2 ) , A 2 = 8 π × 4 2 − 2 = 2 π − 2 , and A 3 = 4 π × 2 2 = π . The area is thus π ( 1 2 − 4 √ 2 ) − 4 = 1 5 . 9 2 7 5 8 0 0 9 0 4 4 4 . . .