Euler's Equipotent MinIntegral Triangle!
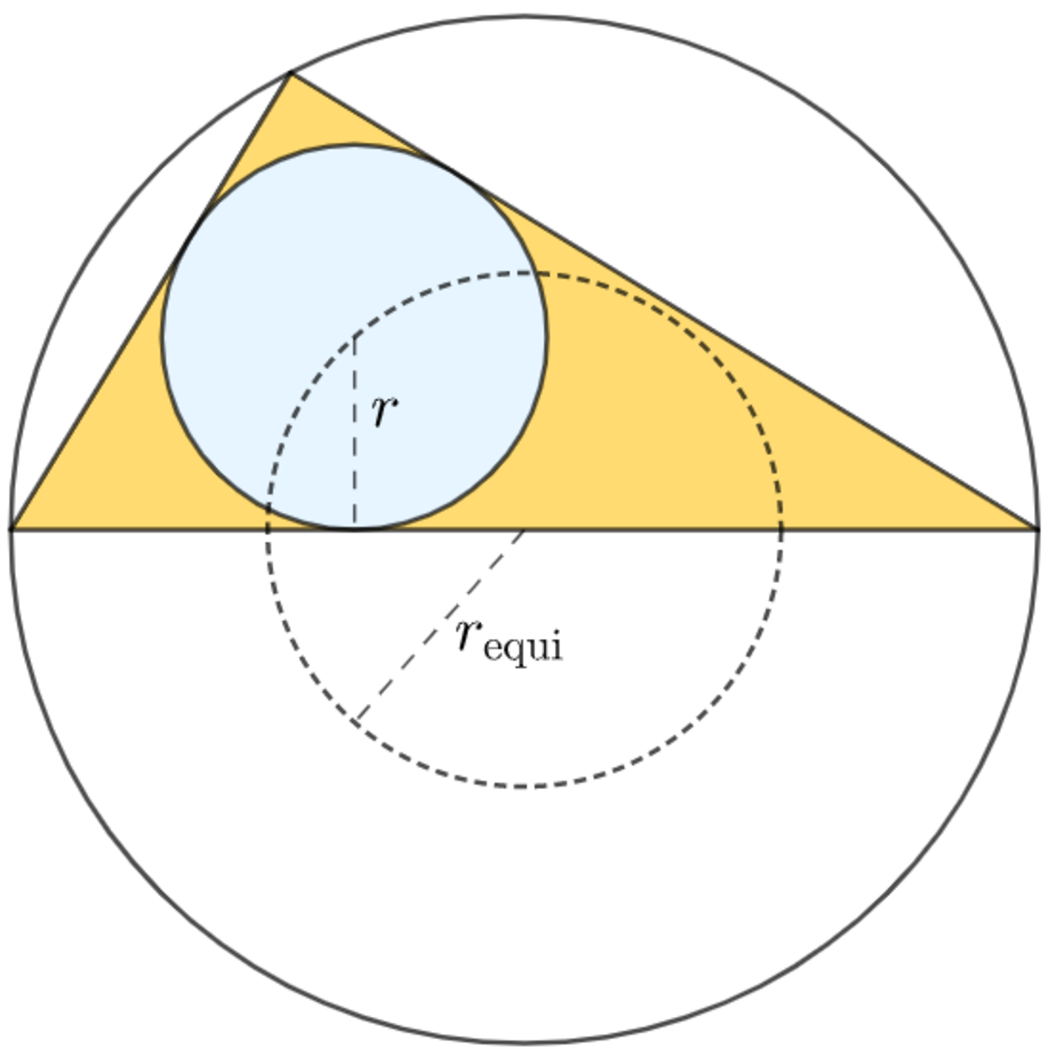
In the circumcircle of integer radius R , there exists an incircle of integer radius r , such that its center lies on the circle also of integer radius r e q u i that is the inradius of an equilateral triangle of the same circumradius. There also exists a right triangle of the inradius r and circumradius R , such that both its area A and its perimeter P are also integers.
If R , r , A , P are positive integers, such that g cd ( R , r , A , P ) = 1 , input the value of A as your answer.
The answer is 57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since the inradius of an equilateral triangle with a circumradius of R is r equi = 2 1 R , and since the distance between the circumcenter and the incenter of a triangle is O I = R ( R − r ) , and since the center of the incircle lies on the circle with a radius of r equi , we know that O I = R ( R − r ) = r equi = 2 1 R , and R ( R − r ) = 2 1 R solves to r = 8 3 R .
Since r must be an integer and r = 8 3 R , let R = 8 k for some integer k . Then r = 8 3 R = 3 k and r equi = 2 1 R = 4 k will also both be integers as required.
Let a and b be the legs of the right triangle and c be the hypotenuse. By Thales's theorem the hypotenuse is also the diameter of its circumcircle, so c = 2 R = 1 6 k , and its inradius is r = 2 1 ( a + b − c ) , or 3 k = 2 1 ( a + b − 1 6 k ) , which rearranges to b = 2 2 k − a .
By the Pythagorean Theorem, a 2 + b 2 = c 2 , or a 2 + ( 2 2 k − a ) 2 = ( 1 6 k ) 2 , which solves to a = ( 1 1 ± 7 ) k .
Then b = 2 2 k − a = 2 2 k − ( 1 1 ± 7 ) k = ( 1 1 ∓ 7 ) k , so the perimeter is P = a + b + c = ( 1 1 ± 7 ) k + ( 1 1 ∓ 7 ) k + 1 6 k = 2 8 k and the area is A = 2 1 a b = 2 1 ⋅ ( 1 1 ± 7 ) k ⋅ ( 1 1 ∓ 7 ) k = 5 7 k 2 .
For the g cd ( R , r , A , P ) = 1 , the g cd ( 8 k , 3 k , 5 7 k 2 , 2 8 k ) = 1 , which means the common factor k = 1 , and if k = 1 , then A = 5 7 k 2 = 5 7 .
If the two non-diameter sides of the right-angled triangle have lengths a , b , then P = a + b + 2 R and A = 2 1 a b are both integers. Thus we deduce that s = a + b must be an integer. Then 4 R 2 = a 2 + b 2 = ( a + b ) 2 − 2 a b = s 2 − 4 A so we deduce that s = 2 σ must be even, and that R 2 = σ 2 − A Since the semiperimeter of the triangle is 2 1 ( a + b + 2 R ) = σ + R , we also have that ( σ + R ) r = A We then observe that r e q u i = 2 1 R . The point of contact of the incircle splits the diameter/hypotenuse into segments of length R + 2 1 ( a − b ) , R + 2 1 ( b − a ) , and so we deduce that r 2 + 4 1 ( a − b ) 2 4 r 2 + a 2 + b 2 − 2 a b 4 r 2 + ( a + b ) 2 − 4 a b 4 r 2 + 4 σ 2 − 8 A = r e q u i 2 = 4 1 R 2 = R 2 = R 2 = R 2 and hence we deduce that R = 2 ρ is even, and so we have the equations 4 ρ 2 = σ 2 − A ( σ + 2 ρ ) r = A r 2 + σ 2 − 2 A = ρ 2 relating ρ , σ , r , A , with R = 2 ρ and P = 2 σ + 4 ρ . But then A = σ 2 − 4 ρ 2 and hence r = σ − 2 ρ , and so we have ( σ − 2 ρ ) 2 + σ 2 − 2 ( σ 2 − 4 ρ 2 ) 1 1 ρ 2 − 4 ρ σ 4 σ = ρ 2 = 0 = 1 1 ρ and hence σ = 1 1 k , ρ = 4 k for some positive integer k . But then R = 8 k and P = 3 8 k . Also A = σ 2 − 4 ρ 2 = 5 7 k 2 and hence r = 3 k . Since R , P , A , r are coprime, it follows that k = 1 , so that R = 8 , P = 3 8 , A = 5 7 and r = 3 . Note that a , b = 1 1 ± 7 .