Evaluate!
Given that a 2 + b 2 = c 2 + d 2 = 1 And also that a c + b d = 0 What is the value of a b + c d ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
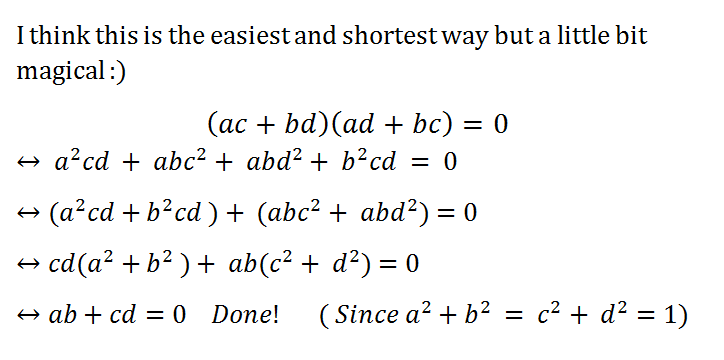
This is the genius I was looking for a ⋅ 0 = 0
What! How did that happen? Miracle!
Sir who are u exactly becoz u solved it in a way a professor solves things
Sir why ad+bc is multiplied in first step
Log in to reply
Because (ac + bd) must equal zero, and anything multiplied by zero must equal zero, than (ac+bd)(ad+bc) must equal zero
Let a = cos θ , b = sin θ , c = cos β and d = sin β .
Substituting in the third equation, we obtain:
cos θ cos β + sin θ sin β = 0
cos ( θ − β ) = 0
Finally, let x = a b + c d , so:
x = cos θ sin θ + cos β sin β
x = 2 1 ( sin 2 θ + sin 2 β )
Use the sum to product formulas:
x = sin ( θ + β ) cos ( θ − β )
x = sin ( θ + β ) ( 0 )
x = 0
In what situations I have to substitute these trigonometric values in an equation?
Log in to reply
Every time you get a 2 + b 2 = 1 then always exists such a θ that a = cos θ and b = sin θ
I took the same approach.
a c + b d = 0
a c = − b d
Squaring both sides
a 2 c 2 = b 2 d 2 -equation p)
Since b 2 = 1 − a 2 , d 2 = 1 − c 2
So putting in equation p)
a 2 c 2 = ( 1 − a 2 ) ( 1 − c 2 )
a 2 c 2 = 1 + a 2 c 2 − a 2 − c 2
a 2 + c 2 = 1
But a 2 + b 2 = 1
Hence b 2 = c 2 Equation q)
Also c 2 + d 2 = 1
Hence a 2 = d 2 Equation r)
We need to find (ab+cd)
so squaring
( a b + c d ) 2 = a 2 b 2 + c 2 d 2 + 2 a b c d
= a 2 c 2 + c 2 a 2 + 2 a b c d Using q) and r)
= 2 a 2 c 2 + 2 a b c d
= 2 a c ( a c + b d )
= 2 a c ∗ 0
= 0
Since ( a b + c d ) 2 = 0
Hence ab+cd=0.
Easiest Way to solve this question
We know (a+b)^2 = a^2 + b^2 + 2ab and (a-b)^2= a^2 + b^2 - 2ab
Using the information given in the problem we deduce
(a+b)^2 = 1+ 2ab Similarly (c+d)^2 = 1+ 2cd
Multiplying the above two eqns we have
(a+b)^2(c+d)^2 = (1+2ab)(1+2cd)
[(a+b)(c+d)]^2 = 1+ 4abcd + 2(ab+cd)
(ad+bc)^2 = 1 + 4abcd + 2(ab+ cd) …… since given that ac+bd=0
(ad+bc)^2 = 1 + 4abcd + 2(ab+ cd) we will name this eqn 1
Again using the information given in the problem we have
(a-b)^2 = 1-2ab and (c-d)^2 = 1- 2cd
Multiplying the above two eqns we get
(a-b)^2(c-d)^2 = (1-2ab)(1-2cd)
[(a-b)(c-d)]^2 = 1+ 4abcd - 2(ab+cd)
[- (ad+bc)]^2 = 1+ 4abcd - 2(ab+cd) …… since given that ac+bd=0
Or (ad+bc)^2 = 1+ 4abcd - 2(ab+cd) we will name this eqn 2
Eqn 1 and eqn 2 represent the same value.
Hence equating them , we get
1 + 4abcd + 2(ab+ cd) = 1+ 4abcd - 2(ab+cd)
Or 4(ab+cd) = 0
And so ab+cd= 0
a,b,c,d can be seen as coordinates of two points A(a.b) and C(c,d) on 2D Cartesian plane.
Both points are on the unit circle since both sums of square are equal to 1.
ac+bd=0 indicates segment OA and OC are perpendicular where O is the origin of the plane.
For a shortcut, take A as (1,0) and C as (0,1) , ab + cd = 0.
My idea, always apply the kiss-principle ;-)
The easiest of the ways is substitution. Let us assume a=c=1 and b=d=0 . Since this assumption satisfies all the conditions mentioned in the question ,it is correct. Therefore, ab+cd = (1)(0) + (1)(0) = 0
x = a b + c d
x 2 = ( a 2 − d 2 ) ( b 2 − c 2 )
W e h a v e a 2 + b 2 − c 2 − d 2 = 0 = > a 2 − d 2 = − ( b 2 − c 2 )
T h u s x 2 = − ( a 2 − d 2 ) 2 = > x = 0
ac+bd=0.
ac= -bd
a/b = -d/c sqare both sides
a^2/b^2 =d^2/c^2 apply componendo
property of proportion
a^2+b^2/b^2= d^2+c^2/c^2
Given a^2+b^2= c^2+d^2=1 we get
1/b^2= 1/c^2
b^2= c^2 implies b= c
So ab+cd =ac+-bd=0
Awswering Ashley Shamidha. When you see the sum of two real quadratic numbers, stay smart to utilize this technique.
Notice that if a = 1 , b = 0 , c = 0 , and d = 1 , then all of the equations will hold true. Because there is only one numerical answer to the problem, the answer must be 1 ⋅ 0 + 0 ⋅ 1 = 0 .