Evaluating algebraic expression

Algebra Level 2

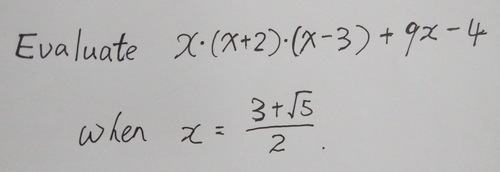Evaluate the expression at given x value. You will need skills of adding, subtracting and multiplying radicals to solve this problem. Challenging but rewarding question. Good Luck and Have Fun.

Note: Round your answer to the thousandth place.


The answer is 14.944.

View wiki
Stanley Guo by Stanley Guo , 34, 中国

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chew-Seong Cheong
Jan 31, 2015

x = 3 + 5 2 ⇒ x 2 − 3 x + 1 = 0 ⇒ x 2 = 3 x − 1 x = \dfrac {3+\sqrt{5}}{2}\quad \Rightarrow x^2 - 3x +1 = 0 \quad \Rightarrow x^2 = 3x-1 .

x ( x + 2 ) ( x − 3 ) + 9 x − 4 = x ( x 2 − x − 6 ) + 9 x − 4 x(x+2)(x-3)+9x-4 = x(x^2-x-6)+9x-4

= x ( 3 x − 1 − x − 6 ) + 9 x − 4 = x ( 2 x − 7 ) + 9 x − 4 =x(3x-1-x-6)+9x-4 =x(2x-7)+9x-4

= 2 x 2 − 7 x + 9 x − 4 = 2 ( 3 x − 1 ) + 2 x − 4 =2x^2-7x+9x-4=2(3x-1)+2x-4

= 6 x − 2 + 2 x − 4 = 8 x − 6 = 4 ( 3 + 5 ) − 6 = 6 + 4 5 = 14.944 =6x-2+2x-4=8x-6=4(3+\sqrt{5})-6=6+4\sqrt{5}=\boxed{14.944}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Elegantly solved.

Stanley Guo - 6 years, 4 months ago

Log in to reply

谢谢！Yes, we should make full use of the fact that x x is a quadratic root.

Chew-Seong Cheong - 6 years, 4 months ago
Stanley Guo
Jan 27, 2015

Add or subtract radicals with different denominators, you will need to find their common denominator then add or subtract. Multiply radicals sometimes can be easier if certain formulas like difference of squares apply.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...