Even a point can be special!

Geometry Level 3

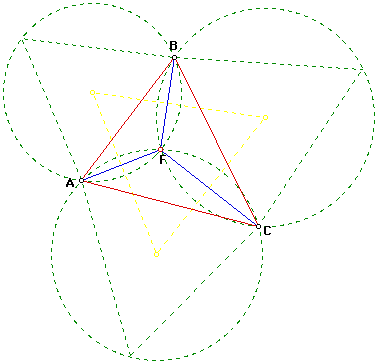
In the figure above , consider a point $F$ such that with comparison to any point inside $\Delta ABC$ , $(FA+FB+FC)$ is minimum.

Then what is the point $F$ known as?

6)Euclid point 2)Torricelli point 8) Both 1),3) 3)Circumcentre 7) Both 1) , 2) 5)Euler point 1)Fermat Point 4)Incentre

1 solution

Michael Mendrin
Jun 2, 2015

There is an interesting "mechanical" demonstration of where this point lies. Let there be 3 small holes at vertices $A, B, C$ . Tie 3 lengths of string, each with a weight (all same weights) attached to the end, each string passing through a vertex, and the knot on the plane of triangle $\Delta ABC$ . Then the weights will pull the strings until no more string can be pulled through any of the holes. A moment's thought leads to the conclusion that the vector forces on the knot must be in equilibrium, and therefore all must make angles of $120$ degrees.

Even a point can be special!

1 solution

0 pending reports