Even split?
Eight circles with equal radii are packed together like this:
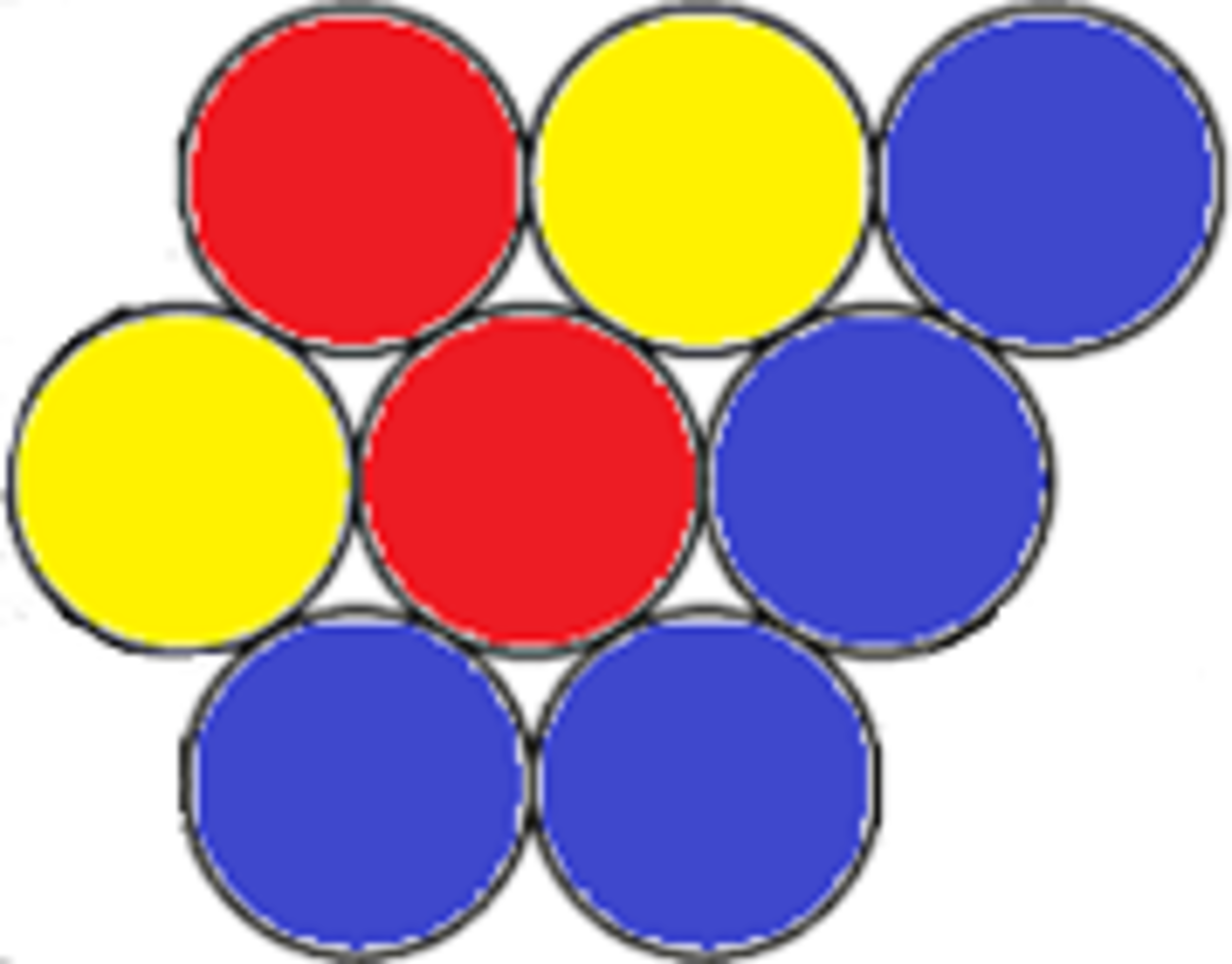
Is there any way to draw a single straight line that has an equal area of red on each side, an equal area of yellow on each side, and and equal area of blue on each side?
Note: The solution, of course, would include different amounts of each color on each side of the line. i.e. There will be twice as much blue as either red or yellow on each side of the line.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider this figure, where A and B are chosen where the circles are tangent.
By symmetry, any point through A will have the same amount of red on each side (and clearly the yellow circles are on opposite sides), and by symmetry, the two blue circles abutting at B will also have similar amounts of area on opposite sides of the line. (In this case they will cut tiny slivers off each circle, but they will have the same area so we are OK. (And of course, the other two blue circles are on entirely opposite sides of the line.
So, yes we can do it as shown above. In fact, this is the only way it can be done.