I don' think questions should be given names.

Algebra Level 3

If x + 1 x = 3 x+\frac { 1 }{ x } =\sqrt { 3 } , find the value of x 18 + x 12 + x 6 + 1 { x }^{ 18 }+{ x }^{ 12 }+{ x }^{ 6 }+1 .


The answer is 0.

View wiki
Vaibhav Prasad by Vaibhav Prasad , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

7 solutions

Manish Dash
May 8, 2015

20 Helpful 0 Interesting 1 Brilliant 0 Confused

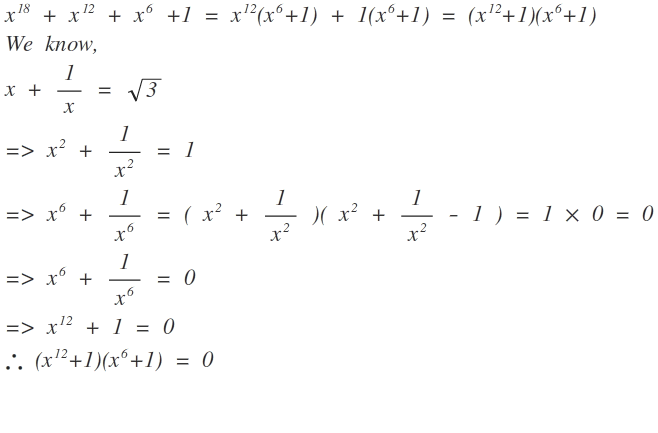
Moderator note:

Yes, well done.

Nice method you got there. Here's another way to look at it:

Take the required expression as S S . From the given equation, we can see that x ≠ 0 , 1 x\neq 0,1 . So, we can regroup our required expression and use finite GP sum formula.

S = x 18 + x 12 + x 6 + 1 = ∑ r = 0 3 ( x 6 ) r = ( x 6 ) 4 − 1 x 6 − 1 S=x^{18}+x^{12}+x^6+1=\sum_{r=0}^3(x^6)^r=\frac{(x^6)^4-1}{x^6-1}

Back to our given equation, cube both sides and with a bit of manipulation, you'll get that,

x 3 + 1 x 3 = 0 ⟹ x 6 + 1 = 0 ⟹ x 6 = ( − 1 ) x^3+\frac{1}{x^3}=0\implies x^6+1=0\implies x^6=(-1)

Use this value of x 6 x^6 to evaluate S S as follows:

S = ( − 1 ) 4 − 1 ( − 1 ) − 1 = 1 − 1 − 2 = 0 S=\frac{(-1)^4-1}{(-1)-1}=\frac{1-1}{-2}=\boxed{0}

Prasun Biswas - 6 years, 1 month ago

I believe there is an error in this method. Specifically, you rely on this line for your solution:

x 6 + 1 x 6 = ( x 2 + 1 x 2 ) ( x 2 + 1 x 2 − 1 ) x^6 + \frac{1}{x^6} = (x^2 + \frac{1}{x^2})(x^2 + \frac{1}{x^2} - 1)

A quick glance shows that the leading term for the result of the right is actually x 4 x^4 , not x 6 x^6 . Working it through completely, you will find that:

( x 2 + 1 x 2 ) ( x 2 + 1 x 2 − 1 ) = x 4 + 1 x 4 − ( x 2 + 1 x 2 ) + 2 = x 4 + 1 x 4 + 1 (x^2 + \frac{1}{x^2})(x^2 + \frac{1}{x^2} - 1) = x^4 + \frac{1}{x^4} - (x^2 + \frac{1}{x^2}) + 2 = x^4 + \frac{1}{x^4}+1

And

x 6 + 1 x 6 ≠ x 4 + 1 x 4 + 1 x^6 + \frac{1}{x^6} \ne x^4 + \frac{1}{x^4}+1

But you do have a good start. Try this out:

x + 1 x = x 2 + 1 x = 3 = > ( x 2 + 1 ) 2 x 2 = 3 = x 4 + 2 x 2 + 1 x 2 = x 2 + 2 + 1 x 2 = 3 x 2 + 1 x 2 = 1 x + \frac{1}{x} = \frac{x^2+1}{x} = \sqrt{3} => \frac{(x^2+1)^2}{x^2} = 3 \\ = \frac{x^4+2x^2+1}{x^2} = x^2 + 2 + \frac{1}{x^2} = 3 \\ x^2 + \frac{1}{x^2} = 1

Next we need x 4 + 1 x 4 x^4 + \frac{1}{x^4} :

1 2 = ( x 2 + 1 x 2 ) 2 = ( x 4 + 1 x 2 ) 2 = x 4 + 2 + 1 x 4 = 1 = > x 4 + 1 x 4 = − 1 1^2 = (x^2 + \frac{1}{x^2})^2 = (\frac{x^4+ 1}{x^2})^2 \\ = x^4 + 2 + \frac{1}{x^4} = 1 \\ => x^4 + \frac{1}{x^4} = -1

Now:

x 2 ( x 4 + 1 x 4 ) = ( − 1 ) ( x 2 ) = > x 6 + 1 x 2 = ( − 1 ) ( x 2 ) = > x 6 = ( − 1 ) ( x 2 + 1 x 2 ) = > x 6 = ( − 1 ) ( 1 ) = − 1 x^2(x^4 + \frac{1}{x^4}) = (-1)(x^2) \\ => x^6 + \frac{1}{x^2} = (-1)(x^2) \\ => x^6 = (-1)(x^2 + \frac{1}{x^2}) \\ => x^6 = (-1)(1) = -1

Now to plug into our equation: x 18 + x 12 + x 6 + 1 = ( x 6 ) 3 + ( x 6 ) 2 + x 6 + 1 = ( − 1 ) 3 + ( − 1 ) 2 + ( − 1 ) + 1 = − 1 + 1 − 1 + 1 = 0 ∴ x 18 + x 12 + x 6 + 1 = 0 x^{18} + x^{12} + x^6 + 1 = {(x^6)}^3 + {(x^6)}^2 + x^6 + 1 \\ = (-1)^3 + (-1)^2 + (-1) + 1 = -1 + 1 - 1 + 1 = 0 \\ \therefore x^{18} + x^{12} + x^6 + 1 = 0

Quintessence Anx - 6 years, 1 month ago
Anandhu Raj
May 7, 2015

Given, x + 1 x = 3 x+\frac { 1 }{ x } =\sqrt { 3 }

Solving for x x , we get that x = 3 2 ± i 2 x=\frac { \sqrt { 3 } }{ 2 } \pm \frac { i }{ 2 }

Multiplying through out by i i ,

⇒ i x = i 3 2 ± − 1 2 \Rightarrow ix=\frac { i\sqrt { 3 } }{ 2 } \pm \frac { -1 }{ 2 }

⇒ i x = ω o r − ω \Rightarrow ix=\omega \quad or\quad -\omega

⇒ x = ω i o r − ω i \Rightarrow x=\frac { \omega }{ i } \quad or\quad -\frac { \omega }{ i }

Substituting the values of x x in x 18 + x 12 + x 6 + 1 { x }^{ 18 }+{ x }^{ 12 }+{ x }^{ 6 }+1 , we get,

− 1 + 1 − 1 + 1 = 0 -1+1-1+1=\boxed{0}

Note: ω i s t h e c u b e r o o t o f u n i t y \omega \quad is\quad the\quad cube\quad root\quad of\quad unity and i = − 1 i=\sqrt { -1 } .

11 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Good work!

@challenge master, Didn't get your point....Would you please explain? How could x x be cube root of unity?

Anandhu Raj - 6 years, 1 month ago

Log in to reply

Sorry, typo. I misinterpreted the question. Well done!

Brilliant Mathematics Staff - 6 years, 1 month ago

Uhmm, @Calvin Lin Sir, There is a typo in the Challenge Master Note

Mehul Arora - 6 years, 1 month ago
Rajdeep Dhingra
May 8, 2015

x + 1 x = 3 x 2 − 3 x + 1 = 0 x = 3 2 ± i 1 2 We can take any value ⇒ x = cos ⁡ ( 30 ) + i sin ⁡ ( 30 ) x + \frac{1}{x} = \sqrt{3} \\ x^2 - \sqrt{3}x + 1 = 0 \\ x = \dfrac{\sqrt{3}}{2} \pm i\dfrac{1}{2} \\ \text{We can take any value} \\ \Rightarrow x = \cos(30) + i\sin(30)

Now We will apply De Moivre's Theorem to evaluate

x 18 + x 12 + x 6 + 1 = ( cos ⁡ ( 30 ) + i sin ⁡ ( 30 ) ) 18 + ( cos ⁡ ( 30 ) + i sin ⁡ ( 30 ) ) 12 + ( cos ⁡ ( 30 ) + i sin ⁡ ( 30 ) ) 6 + 1 Applying theorem we get = cos ⁡ ( 18 × 30 ) + i sin ⁡ ( 18 × 30 ) + cos ⁡ ( 12 × 30 ) + i sin ⁡ ( 12 × 30 ) + cos ⁡ ( 6 × 30 ) + i sin ⁡ ( 6 × 30 ) + 1 = − 1 + 0 + 1 + 0 − 1 + 0 + 1 0 x^{18} + x^{12} + x^6 + 1 \\ = (\cos(30) + i\sin(30))^{18} + (\cos(30) + i\sin(30))^{12} +\\ ( \cos(30) + i\sin(30))^6 + 1 \\ \text{Applying theorem we get} \\ = \cos(18\times30) + i\sin(18\times30) + \cos(12\times30) + i\sin(12\times30) + \\ \cos(6\times30) + i\sin(6\times30) + 1 \\ = -1 + 0 + 1 + 0 -1 + 0 + 1 \\ \boxed{0}

7 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

You can have a slight improvement. Hint: all the powers of x x are a multiple of 6 6 .

Javier Sanjuan
May 8, 2015

x 18 + x 12 + x 6 + 1 = ( x 12 + 1 ) ( x 6 + 1 ) = x 9 ( x 6 + 1 x 6 ) ( x 3 + 1 x 3 ) Then, given: x + 1 x = 3 x 2 + 1 x = 3 ( x 2 + 1 ) 3 x 3 = 3 3 x 6 + 3 x 4 + 3 x 2 + 1 x 3 = 3 3 x 3 + 3 x + 3 x + 1 x 3 = 3 3 x 3 + 1 x 3 = 0 ⇒ x 18 + x 12 + x 6 + 1 = 0 x^{18}+x^{12}+x^6+1=(x^{12}+1)(x^6+1)=x^9(x^6+\frac{1}{x^6})(x^3+\frac{1}{x^3}) \\ \text{Then, given:}\\x+\frac{1}{x}=\sqrt{3} \\ \frac{x^2+1}{x}=\sqrt{3}\\ \frac{(x^2+1)^3}{x^3}=3\sqrt{3} \\ \frac{x^6+3x^4+3x^2+1}{x^3}=3\sqrt{3}\\ x^3+3x+\frac{3}{x}+\frac{1}{x^3}=3\sqrt{3} \\ x^3+\frac{1}{x^3}=0 \\ \Rightarrow x^{18}+x^{12}+x^6+1=0

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

It's easier to start with cubing the equation x + 1 x = 3 x + \frac 1x = \sqrt 3 . Most people opted for the complex number approach, and you didn't. Nicely done!

x + 1 x = 3 . ∴ x ≠ 0. ( x + 1 x ) 3 = x 3 + 1 x 3 + 3 ∗ 1 ∗ ( x + 1 x ) . ⟹ x 3 + 1 x 3 + 3 ∗ 1 ∗ 3 = 3 3 . ∴ x 3 + 1 x 3 = 0. ∴ x 6 = − 1 , x 12 = 1 , x 18 = − 1. x+\dfrac 1 x =\sqrt 3. ~~\therefore x\neq0.\\\left (x+\dfrac 1 x \right )^3=x^3+\dfrac 1 {x^3}+3*1*( x+\dfrac 1 x).\\\implies~x^3+\dfrac 1 {x^3} +3*1*\sqrt 3=3\sqrt 3 .\\ \therefore~{x^3}+\dfrac 1 {x^3}=0.\\\therefore~x^6=-1,~~~~x^{12}=1,~~~x^{18}=-1.\\ ∴ x 18 + x 12 + x 6 + 1 = − 1 + 1 − 1 + 1 = 0 \therefore x^{18}+x^{12}+x^6+1=-1+1-1+1= ~~~~~~~~~~~~\color{#D61F06}{\Large 0}

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Hem Shailabh Sahu
May 10, 2015

We are given : x + 1 x = 3 . . . ( 1 ) x+\frac{1}{x}=\sqrt{3}...(1) Required expression : x 18 + x 12 + x 6 + 1 = ( x 6 + 1 ) ( x 12 + 1 ) = x 3 ( x 3 + 1 x 3 ) ( x 12 + 1 ) . . . ( 2 ) x^{18}+x^{12}+x^6+1=(x^6+1)(x^{12}+1)=x^{3}(x^3+\frac{1}{x^3})(x^{12}+1)...(2) Cubing both the sides of (1), ( x + 1 x ) 3 = ( 3 ) 3 (x+\frac{1}{x})^{3}=(\sqrt{3})^{3} ⇒ x 3 + 1 x 3 + 3 ( x ) ( 1 x ) ( x + 1 x ) = 3 3 \Rightarrow x^3+\frac{1}{x^3}+3(x)(\frac{1}{x})(x+\frac{1}{x})=3\sqrt{3} Using (1), ⇒ x 3 + 1 x 3 = 0... ( 3 ) \Rightarrow x^3+\frac{1}{x^3}=0...(3) Therefore, using (3), the value of required expression (2) = x 3 ( x 3 + 1 x 3 ) ( x 12 + 1 ) = 0 =x^{3}(x^3+\frac{1}{x^3})(x^{12}+1)=\boxed{0}

:D

1 Helpful 0 Interesting 0 Brilliant 0 Confused
L N
May 10, 2015

x + 1 x = 3 x + \frac{1}{x} = \sqrt{3}

x 2 + 1 = 3 x x^2 + 1 = \sqrt{3}x

( x 2 + 1 ) 2 = 3 x 2 (x^2 + 1)^2 = 3x^2

x 4 + 2 x 2 + 1 = 3 x 2 x^4 + 2x^2 + 1 = 3x^2

x 4 − x 2 + 1 = 0 x^4 - x^2 + 1 = 0

Let z = x 2 z = x^2

z 2 − z + 1 = 0 z^2 - z + 1 = 0

z = ( − 1 ) 1 3 z = (-1)^{\frac{1}{3}}

x = ( − 1 ) 1 6 x = (-1)^{\frac{1}{6}}

There are other solutions for z z and x x , however this one does give a real valued solution as needed. Plug in the value of x x just found to get 0 0

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...