Everybody, let's roll!

Classical Mechanics Level 3

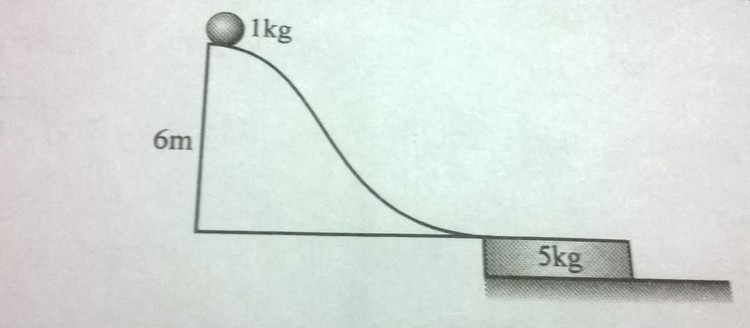A small disc of mass 1kg slides down a smooth hill of height 6 m without initial velocity and gets onto a plank of mass 5 kg lying on a smooth horizontal plane at the base of hill as shown in the figure. Due to friction between the disc and the plank , disc slows down and after some time moves as one piece with the plank . Find out the magnitude of total work (in joule) performed by the friction forces in this process.

50 100 64 300

Prashant Kr by Prashant Kr , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Parag Zode
Mar 19, 2015

Using Work -Energy theorem ,

W f = K f − K i W_{f}=K_{f}-K_{i} where

W f W_{f} =Final work done.

K f K_{f} =Final kinetic energy.

K i K_{i} =Initial kinetic energy.

W f = 1 2 ( m + M ) V 2 − 1 2 m v o 2 W_{f}=\dfrac{1}{2}(m+M)V^{2} - \dfrac{1}{2}mv_{o}^{2}

= − 1 2 m M v o 2 m + M \dfrac{-1}{2}\dfrac{mMv_{o}^{2}}{m+M}

= − m M g h m + M -\dfrac{mMgh}{m+M} , since v o 2 = 2 g h v_{o}^{2}=2gh

Substituting m=1 kg \text{m=1 kg} , M=5 kg \text{M=5 kg} , h h = 6 6 and g g = 10 10 ,we get W f = − 50 J W_{f}=\boxed{-50J}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...