Everything Touches, Part 2
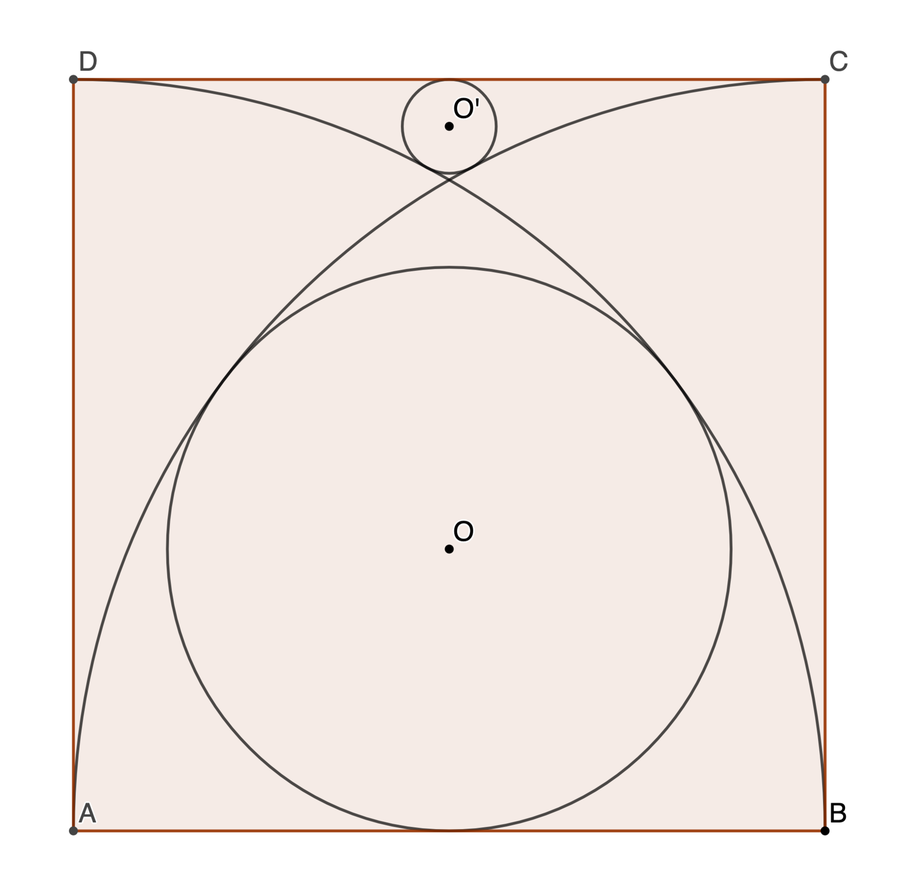
A B C D is a square with side length 16. Two quadrants are centered at A and B . Find the sum of the radii of the two inscribed circles.
The answer is 7.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
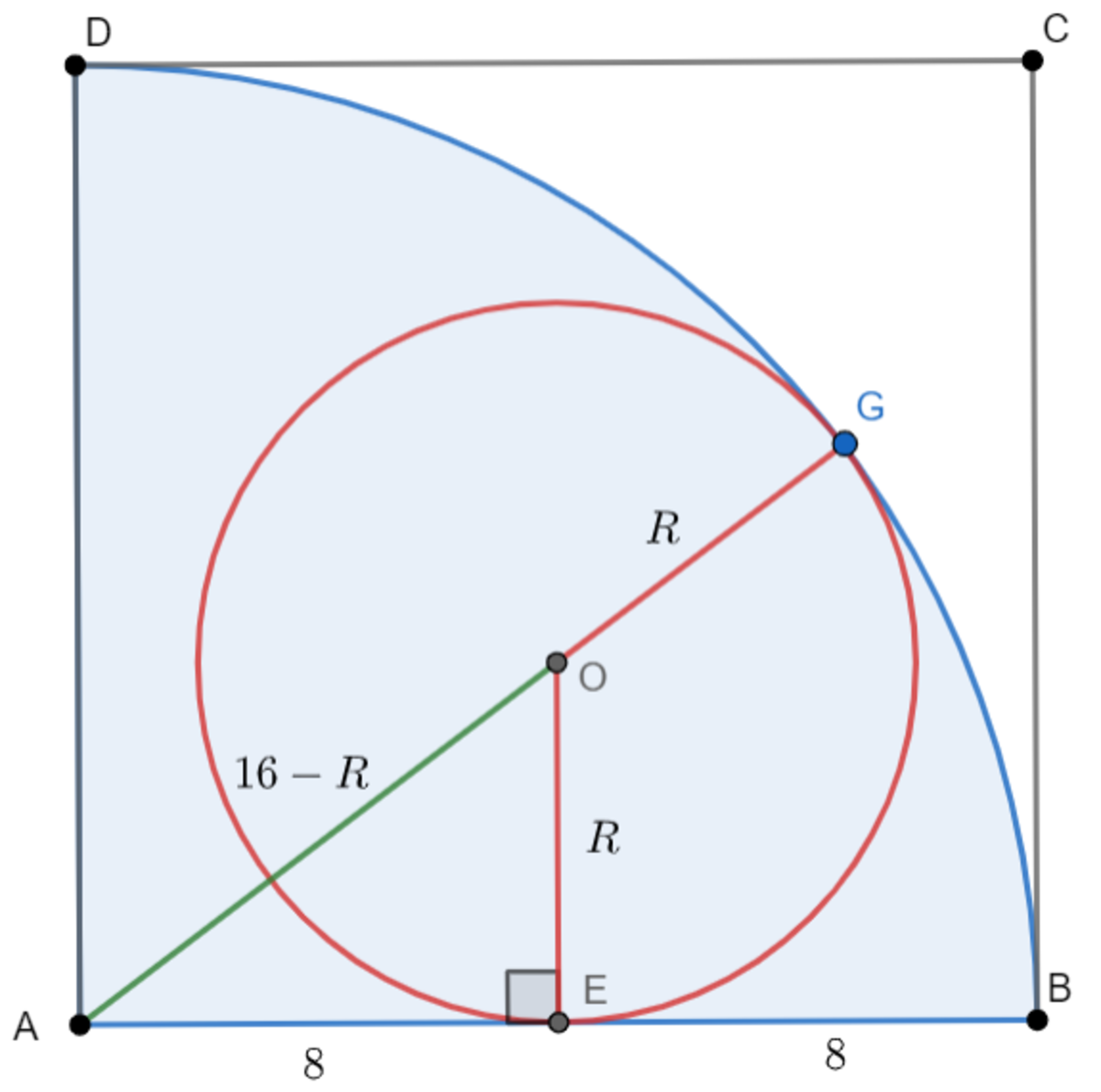
Claim:
The larger circle centered at
O
has radius
6
.
 Proof:
Note that the points
A
,
O
and the point of contact,
G
are all collinear. Let the radius of the larger circle be
R
. In the figure above, applying the Pythagorean Theorem in
△
A
E
O
,
A
E
2
+
E
O
2
=
O
A
2
⟹
8
2
+
R
2
=
(
1
6
−
R
)
2
=
1
6
2
−
3
2
R
+
R
2
⟹
R
=
3
2
1
6
2
−
8
2
=
6
Proof:
Note that the points
A
,
O
and the point of contact,
G
are all collinear. Let the radius of the larger circle be
R
. In the figure above, applying the Pythagorean Theorem in
△
A
E
O
,
A
E
2
+
E
O
2
=
O
A
2
⟹
8
2
+
R
2
=
(
1
6
−
R
)
2
=
1
6
2
−
3
2
R
+
R
2
⟹
R
=
3
2
1
6
2
−
8
2
=
6
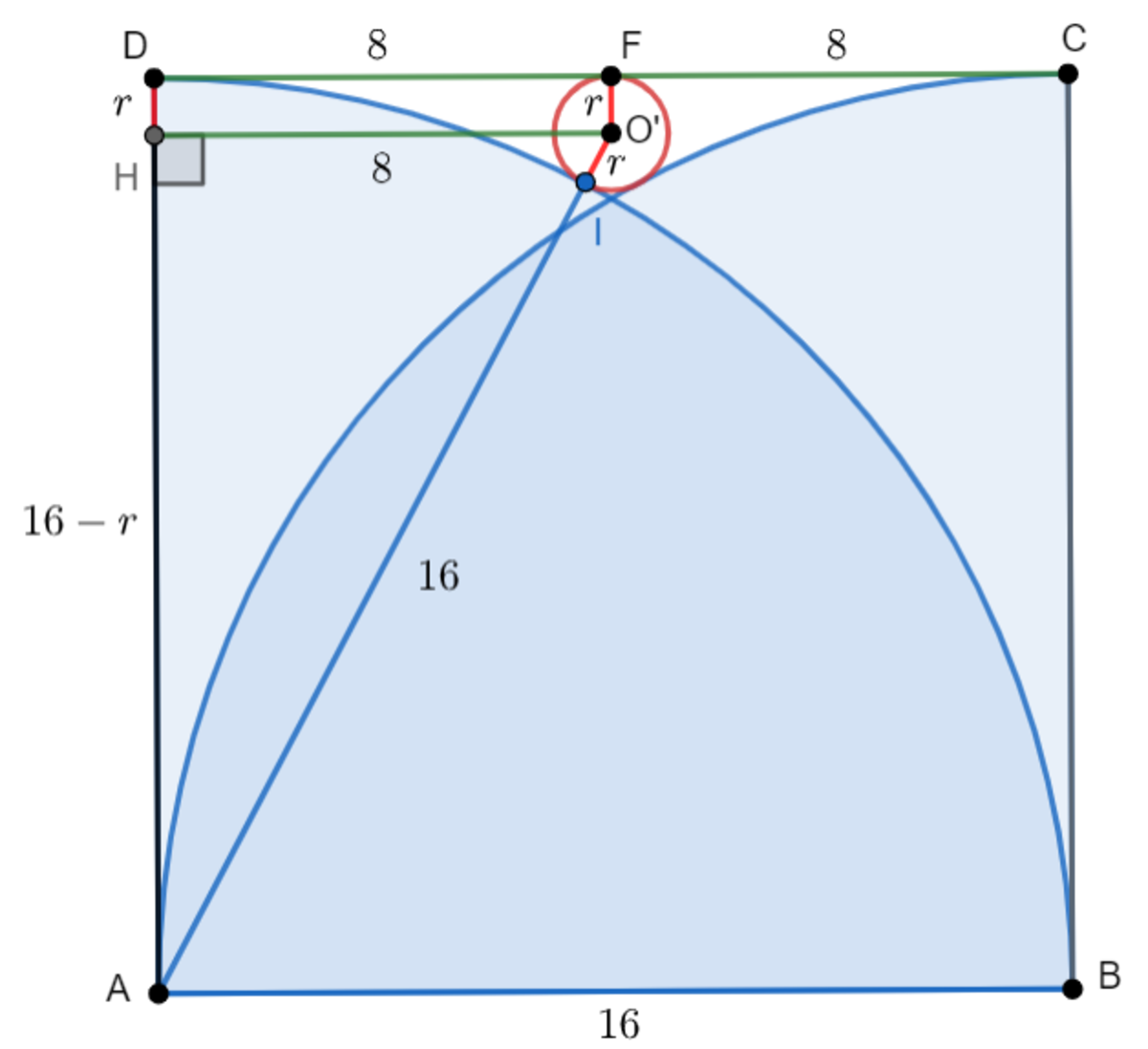
Claim:
The smaller circle centered at
O
′
has radius
1
.
 Proof:
Note that the points
A
,
O
′
and the point of contact,
I
are all collinear. Let the radius of the smaller circle be
r
. In the figure above, applying the Pythagorean Theorem in
△
A
H
O
′
,
O
′
H
2
+
A
H
2
=
O
′
A
2
⟹
8
2
+
(
1
6
−
r
)
2
=
(
1
6
+
r
)
2
⟹
8
2
+
1
6
2
−
3
2
r
+
r
2
=
1
6
2
+
3
2
r
+
r
2
⟹
r
=
6
4
8
2
=
1
Proof:
Note that the points
A
,
O
′
and the point of contact,
I
are all collinear. Let the radius of the smaller circle be
r
. In the figure above, applying the Pythagorean Theorem in
△
A
H
O
′
,
O
′
H
2
+
A
H
2
=
O
′
A
2
⟹
8
2
+
(
1
6
−
r
)
2
=
(
1
6
+
r
)
2
⟹
8
2
+
1
6
2
−
3
2
r
+
r
2
=
1
6
2
+
3
2
r
+
r
2
⟹
r
=
6
4
8
2
=
1
Therefore, the sum of the radii of the two inscribed circles is R + r = 7
Let the radius of the small and big circles be r and R respectively, M and N be the midpoints of C D and A B respectively, and P Q be a diameter of the big circle such that A , P , O , and Q are colinear,
By tangent-secant theorem , we have:
A P ⋅ A Q ( 1 6 − 2 R ) ⋅ 1 6 8 − R ⟹ R = A N 2 = 8 2 = 2 = 6
By Pythagorean theorem , we have:
O ′ A 2 ( 1 6 + r ) 2 ( 1 6 + r ) 2 − ( 1 6 − r ) 2 6 4 r ⟹ r = A N 2 + O ′ N 2 = 8 2 + ( 1 6 − r ) 2 = 6 4 = 6 4 = 1
Therefore r + R = 1 + 6 = 7 .