Everything Touches
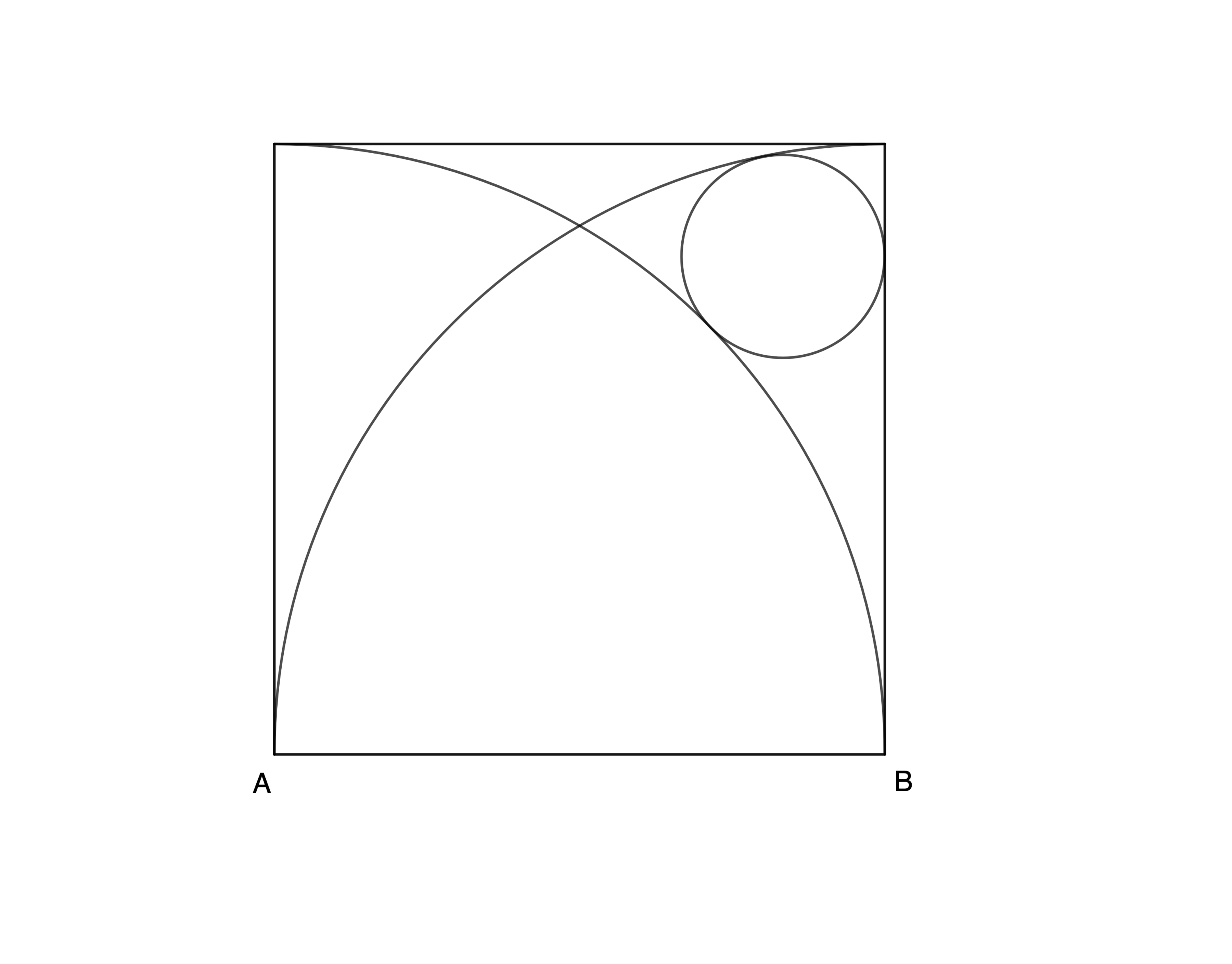
The figure depicts a square with quarter circles centered at A and B . A small circle touches the quarter circles as well as one side of the square. What is the ratio of the A B to the radius of the small circle.
The answer is 6.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let A B = 1 and A be the origin ( 0 , 0 ) of the x y -plane. Then the equations for the quadrants centered at A and B are:
{ Q A : Q B : x 2 + y 2 = 1 ( x − 1 ) 2 + y 2 = 1
Let the center of the small circle be C ( x 0 , y 0 ) and its radius r . Then C satisfies the following system of equations:
⎩ ⎪ ⎨ ⎪ ⎧ x 0 2 + y 0 2 = ( 1 + r ) 2 ( x 0 − 1 ) 2 + y 0 2 = ( 1 − r ) 2 x 0 = 1 − r . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
Then we have:
( 1 ) − ( 2 ) : x 0 2 − ( x 0 − 1 ) 2 2 x 0 − 1 2 − 2 r − 1 ⟹ r = ( 1 + r ) 2 − ( 1 − r ) 2 = 4 r = 4 r = 6 1 From ( 3 ) : x 0 = 1 − r
Therefore, r A B = 6 .
r denotes the radius and O is the center of small circle, C is the point where small circle tangents square. Let ∠ A B O = α , ∠ C B O = β , A B = 1
A O B O cos α A O 2 ( 1 + r ) 2 r = 1 + r = 1 − r = sin β = 1 − r r = A B 2 + B O 2 − 2 ⋅ A B ⋅ B O cos α = 1 + ( 1 − r ) 2 − 2 ⋅ 1 ⋅ ( 1 − r ) 1 − r r = 6 1