Everything Unique
× A D B C E + D F H E G I
If all of those variables contain distinct positive single-digit integers, input the concatenation D E H I as your answer. For instance, if D E = 1 2 and H I = 3 4 , input 1 2 3 4 .
The answer is 6893.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The only way is 17*4=68 68+25=93
Unique solution for (10A + B) X C = [10D + E] + (10F + G) = [10H + I], with A ~ I representing distinct digital positive integers.
10D + E ≤ 98 - 12 = 86
As B < 10A
and
B / (10A + B) is at most 9/19 < 1/2, then
BC < C(10A + B)/2 = (10D + E)/2 = 86/2 = 43
Now let's consider the parity of the last digits of the numbers, namely B, C, E, G & I. Let P represent them being even and Q odd for the equation of { I = G + E <== BC } .
There are 4 possibilities :
1) P = P + P <== PQ or QP
2) P = Q + Q <== QQ
3) Q = P + Q <== QQ
4) Q = Q + P <== PQ or QP or PP
1) P = P + P <== PQ or QP
a) 2 = 4 + 8 with 6 x 3 or 3 x 6
b) 2 = 8 + 4 with 6 x 9 or 9 x 6
c) 4 = 6 + 8 with 2 x 9 or 9 x 2
d) 4 = 8 + 6 with 2 x 3 or 3 x 2
e) 6 = 4 + 2 with 8 x 9 or 9 x 8
f) 6 = 2 + 4 with 8 x 3 or 3 x 8
g) 8 = 6 + 2 with 4 x 3 or 3 x 4
h) 8 = 2 + 6 with 4 x 9 or 9 x 4
We can see that the sole odd number in these possibilities here can only either be 3 or 9. Since we have already depleted all the even digit reserves in the possibilities, H, F and D must all be odds, so in our addition part there should be a carryover from G and E, and with this we can reject the possibilities from e) ~ h). Furthermore, since we already found BC < 43, possibility b) with 6 x 9 = 54 > 43 ≠ BC is also rejected. Looking at a) & c) with their BC = 18 = 10 + 8 with odd carryover, their C must be the even ones out of the pairs (6,3) and (2,9), and the C in d) must be odd by the same reason (to enable an odd D after the multiplication AC + carryover). With only a few odd digits left and the limit of 10D + E ≤ 86, it's easy to check & see that none of these three works.
2) P = Q + Q <== QQ
3) Q = P + Q <== QQ
Both of the possibilities above involve the multiplication of two odd numbers, but limitations of a single unique solution made our search easier.
a) 1 = 3 x 7 or 7 x 3 ( even carryover)
b) 3 = 9 x 7 or 7 x 9 ( even carryover)
c) 7 = 3 x 9 or 9 x 3 ( even carryover)
===> { 5 can't be involved in these multiplication or another 5 would be necessary while 9 can only be produced by self-multiplication with 1 or squaring other digits }
b) is rejected by BC < 43. With both a) and c), either will make use of 3 & 7 in the multiplication part. Also, with their even carryover, A & D will have to be of the same parity, but in these cases of 2) & 3), 4 of the digit / ones places are already taken by the odd integers leaving A & D to be both even. A ≥ 2 making the product in c) exceed 86 and even for a) with 3 x 27 = 81, H ≤ 9 is impossible if F ≥ 4 and D = 8.
With all the above cases proven fruitless, we're left to check if the last one would somehow workable.
4) Q = Q + P <== PQ or QP
Looking at the multiplication first,
2 <== { 4x3 or 6x7 or 8x9 }
4 <== { 2x7 or 6x9 or 8x3 }
6 <== { 2x3 or 4x9 or 8x7 }
8 <== { 2x9 or 4x7 or 6x3 }
Now, consider the limit of BC < 43 and weed out the impossibilities.
2 <== { 4x3 or 6x7 }
4 <== { 2x7 or 8x3 }
6 <== { 2x3 or 4x9 }
8 <== { 2x9 or 4x7 or 6x3 }
For multiplications with a B-C combo containing a digit ≥ 7, we can safely assume that the smaller number of the pair would have to be C or the product might cross over to the hundreds when 12 as the least value of 10A + B can even reach 84 (12 x 7) in just the multiplication stage and no way to be contained within 98 sum with the two smallest digits already taken out.
Also for a B-C combo with B + C > 10, it almost always leading to A = 1. As such, for B + C > 10, we need to aim for 10D + E = (10A + B) x C ≤ 98 - 23 = 75, with BC < 38. By these stricter conditions, 6 x 7 = 42 ≥ 38 and 4x9's 19 x 4 = 76 > 75 can be eliminated.
Our final results to be brute forced over would be in the list below :
i) 2 <== { 4x3 }
ii) 4 <== { 2x7 or 8x3 }
iii) 6 <== { 2x3 }
iv) 8 <== { 2x9 or 4x7 or 6x3 }
i) 2 <== { 4x3 }
If A ≠ 1, then A ≥ 5, but even A = 5 can accommodate for either of the C = 3 or C = 4 (A should be ≤ 2 for both Cs). Then A = 1. Brute forcing 14 x 3 on one hand, we get a result of 42 with B = D, while 13 x 4 = 52 uses up all the smallest 5 digits for a 3-digit total sum since F is coincidentally pushed to take F ≥ 6.
ii) 4 <== { 2x7 or 8x3 }
C = 2 forces the limit A ≤ 4 while C = 3 --> A ≤ 2. So it could go 2 ways for each : 17 x 2 = 34 or 37 x 2 = 74 or 18 x 3 = 54 or 28 x 3 = 84. Where A ≠ 1, we get results of B = D.
17 x 2 = 34 { waiting list : 5, 6, 8 & 9 }
A difference of 4 can only be found between 5 & 9, so these should be G & I respectively, but 3 (tens from product 34) + 6 = 9 > 8 from the remaining digits.
18 x 3 = 54 { waiting list : 2, 6, 7 & 9 }
A difference of 4 can only be found between 2 & 6, but these aren't odd digits as we've posited earlier.
iii) 6 <== { 2x3 }
Again, C = 2 forces the limit A ≤ 4 while C = 3 --> A ≤ 2, but neither C can have A = 1 since this BC being < 10 (thus the no carryover) that will reduce it into C = D. It could only go 1 way : 43 x 2 = 86 with F = 1 and H = 9 but no solutions for G & I between the leftovers 5 & 7.
iv) 8 <== { 2x9 or 4x7 or 6x3 }
Again, C = 2 forces the limit A ≤ 4 while C = 3 or 4 --> A ≤ 2.
1) 19 x 2 = 38
2) 39 x 2 = 78
3) 49 x 2 = 98
4) 17 x 4 = 68
5) 27 x 4 = 108 X (limit exceeded) X
6) 13 x 6 = 78
7) 16 x 3 = 48
8) 26 x 3 = 78
Case 5) invalid for a product > 100. Case 3) invalid for repeated 9 in B and D. Case 2) invalid for the product of 78 not having a digit larger than themselves to makeup for the tens of the total sum (9 already taken out to be a B).
1) 19 x 2 = 38 { waiting list : 4, 5, 6 & 7 }
If odd digits were to be G & I, then 3 (tens from product 38) + 4 = 7 > 6 from the remaining digits.
4) 17 x 4 = 68 { waiting list : 2, 3, 5 & 9 }
A difference of 8 can only be found between 5 & 3, so these should be G & I respectively, and also 6 (tens from product of 68) + 2 = 8 < 9, which is totally okay since the missing (but not extra) difference of one can be explained by the carryover of 1.
6) 13 x 6 = 78 { waiting list : 2, 4, 5 & 9 }
No difference of 8 between the two odd digits in waiting list.
7) 16 x 3 = 48 { waiting list : 2, 5, 7 & 9 }
7 would have to be either G or I, but with F = 2, H can only be 7, and thus the contradiction.
8) 26 x 3 = 78 { waiting list : 1, 4, 5 & 9 }
4 can only be F as an even digit less than the tens of the product 78, but 78 + (40+) > 100.
Answer :
17 x 4 = 68 + 25 = 93
Looking at a) & c) with their BC = 18 = 10 + 8 with odd carryover, their C must be the even ones out of the pairs (6,3) and (2,9), and the C in d) must be odd by the same reason (to enable an odd D after the multiplication AC + carryover). With only a few odd digits left and the limit of 10D + E ≤ 86, it's easy to check & see that none of these three works.
13 x 6 = 78 + (smallest possible number 24) > 95
19 x 2 = 38 + (smallest possible number 45) > 76
39 x 2 = 78 + (smallest possible number 14) > 65
For 4 = 8 + 6 from 2 x 3, without any carryover 3 cannot be a multiplier of 1 (else getting another 3) and the next available odd number is already 5, too big to be useful.
4) Q = Q + P <== PQ or QP or PP
Looking at the multiplication first,
2 <== { 4x3 or 6x7 or 8x9 } or {4x8}
4 <== { 2x7 or 6x9 or 8x3 }
6 <== { 2x3 or 4x9 or 8x7 } or {2x8}
8 <== { 2x9 or 4x7 or 6x3 } or {4x2}
As the above, we should use the smaller pair as C whenever we have the two largest evens as one of the pair to contain the product and ultimately the resulting sum under 98.
18 x 4 = 72 + (smallest possible number 35) > 96
18 x 2 = 36 + (smallest possible number 45) = 81 ==> Usable digits : 4, 5, 7 & 9 ==> 36 + 57 = 93 ≠ 94 (missed by 1!)
38 x 2 = 76 + (smallest possible number 14) = 90 ==> Usable digits : 1, 4, 5 & 9 ==> 76 + 15 = 91 ≠ 94 (missed by 3!)
34 x 2 = 68 + (smallest possible number 15) = 83 ==> Usable digits : 1, 5, 7 & 9 ==> 68 + 17 = 85 ≠ 95 (missed by 10)
32 x 4 = 128 > 98
When a grid is coloured red, it means that the letter it corresponds to cannot take the value of the number it corresponds to. For example, if grid A 5 is coloured red, than A = 5 .
Now we can colour grids A 0 to I 0 red since all digits are positive. Obviously, C = 1 as it would produce same digits.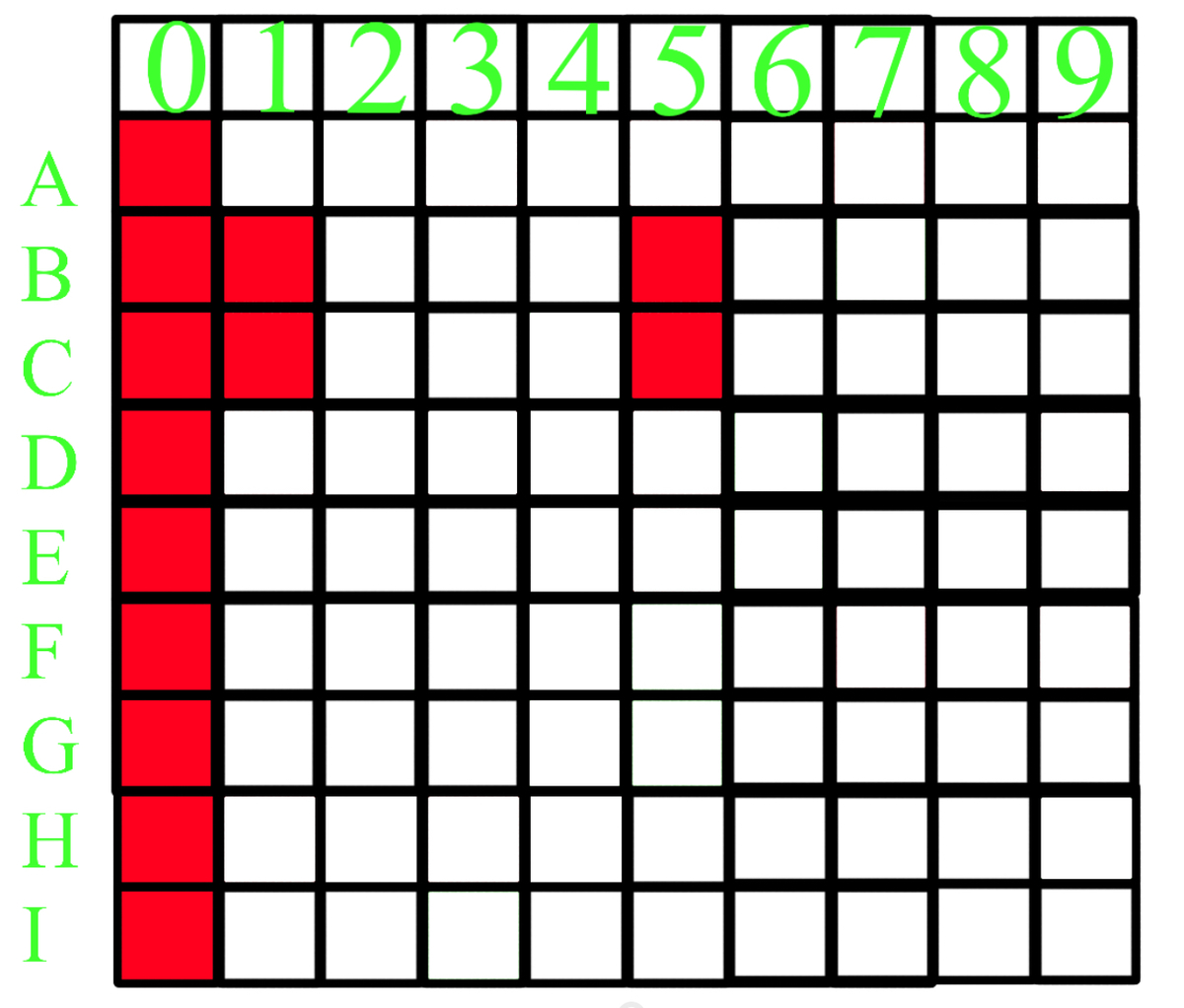
C = 5 as well. When C = 5 and B is even, E = 0 , but all digits are positive. When C = 5 and B is odd, E = C = 5 , now contradicting the fact that all digits are distinct. ∴ C = 5 .
Using the same logic, B = 1 and B = 5 .
Next, since C ≥ 2 and A B × C = D E < 1 0 0 , A B < 5 0 . ∴ A < 5 .
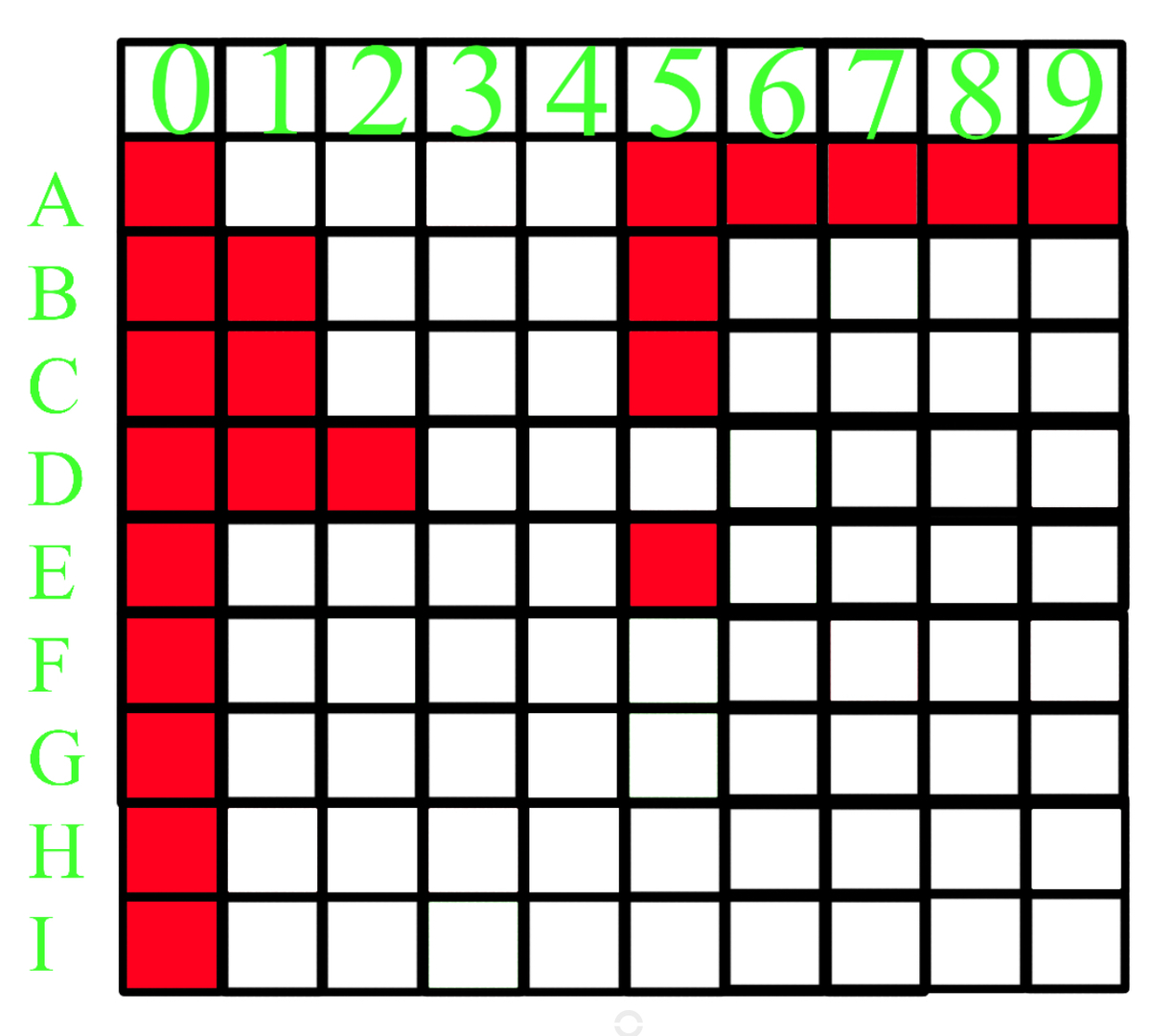 More analysis to the problem cannot help us find the exact values of the digits. Instead, we must solve it by brute force. Calculating by hand should take less time than writing and running a program. Here is my result:
×
1
6
7
4
8
+
6
2
9
8
5
3
More analysis to the problem cannot help us find the exact values of the digits. Instead, we must solve it by brute force. Calculating by hand should take less time than writing and running a program. Here is my result:
×
1
6
7
4
8
+
6
2
9
8
5
3
The smallest value of D E comes from multiplying 1 − by 2 . The result should be greater than 3 0 to prevent same digits. Therefore D ≥ 3 .