Ew Ugly Diagram

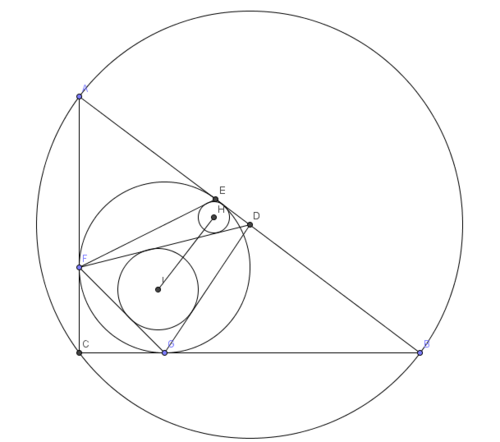Let $ABC$ be a right triangle with right angle at $C$ such that $AC = 3$ and $BC = 4$ . The circumcircle of $ABC$ has center $D$ and the incircle of $ABC$ touches the sides at points $E, F,$ and $G$ , with $E$ on $AB$ , $F$ on $AC$ , and $G$ on $BC$ . Triangles $EDF$ and $FGD$ have incenters $H$ and $I$ , respectively. If $HI = k$ , then find $\lfloor 100 k \rfloor$ .

Details and assumptions:

Geogebra users, stay away. (Unless you're just harmlessly making a diagram for your own use, then you're welcome to answer.)

Once you find the exact answer, you may use a calculator.