Exactly one point
Four points are chosen uniformly and at random inside a circle of radius 2.
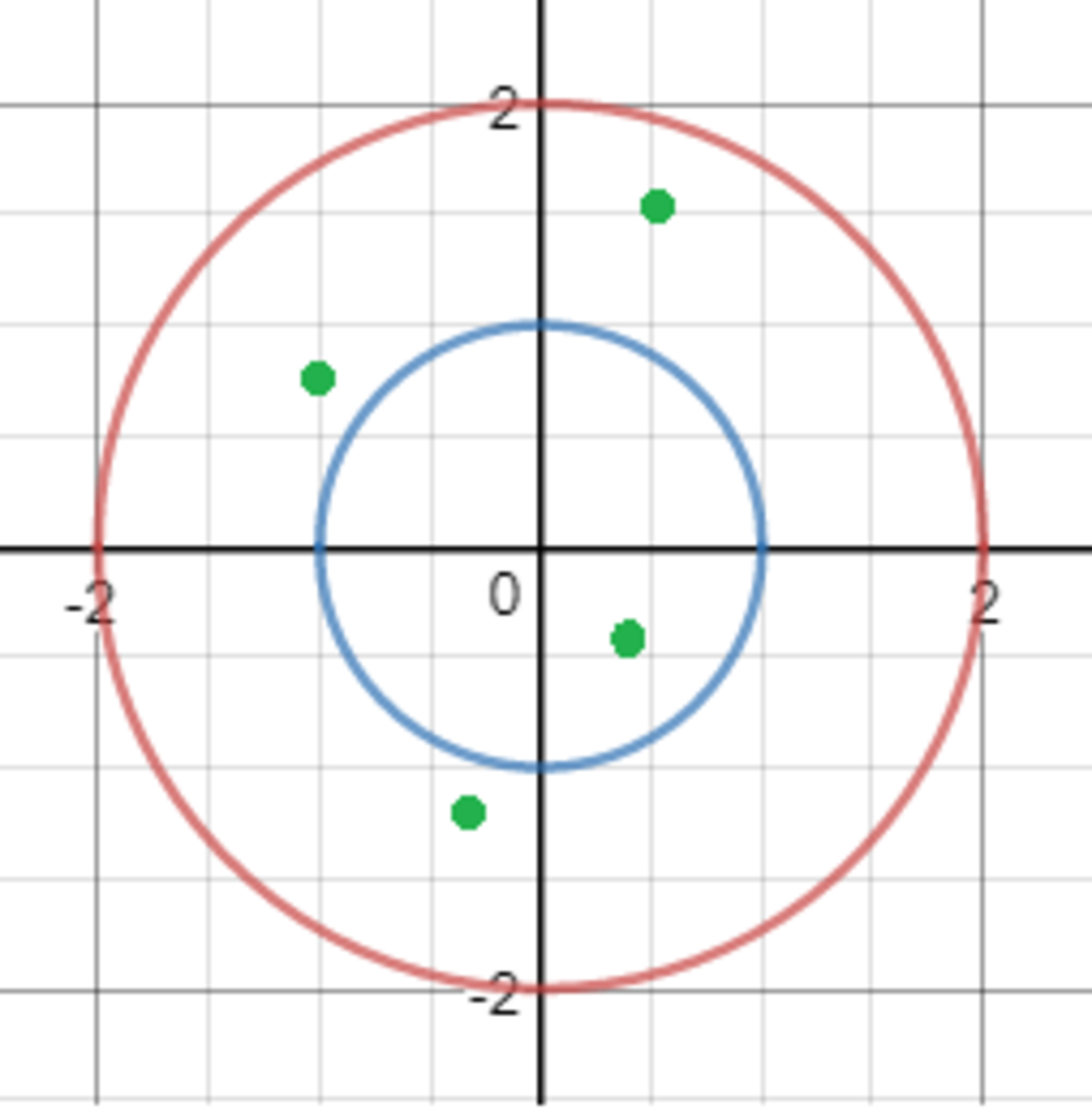
If the probability that exactly one point is within one unit from the center of the circle is given by where and are coprime positive integers, then what is ?
The answer is 91.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that a circle of radius 2 is 4 times as big as a circle of radius 1. So, each point has a 4 1 of being inside the inner circle (or within one from the center), and 4 3 probability of not being within one from the center.
So, for each point, the probability that it is the only point within one unit of the center is given by:
P each point = 4 1 ( 4 3 ) 3
since there is a 4 1 probability that it is within one from the center of the circle, and there is a 4 3 probability that each of the other three isn't within one unit from the center.
And, there are four points to consider, so the total probability is given by
P = 4 P each point = 4 4 1 ( 4 3 ) 3 = 6 4 2 7
2 7 + 6 4 = 9 1