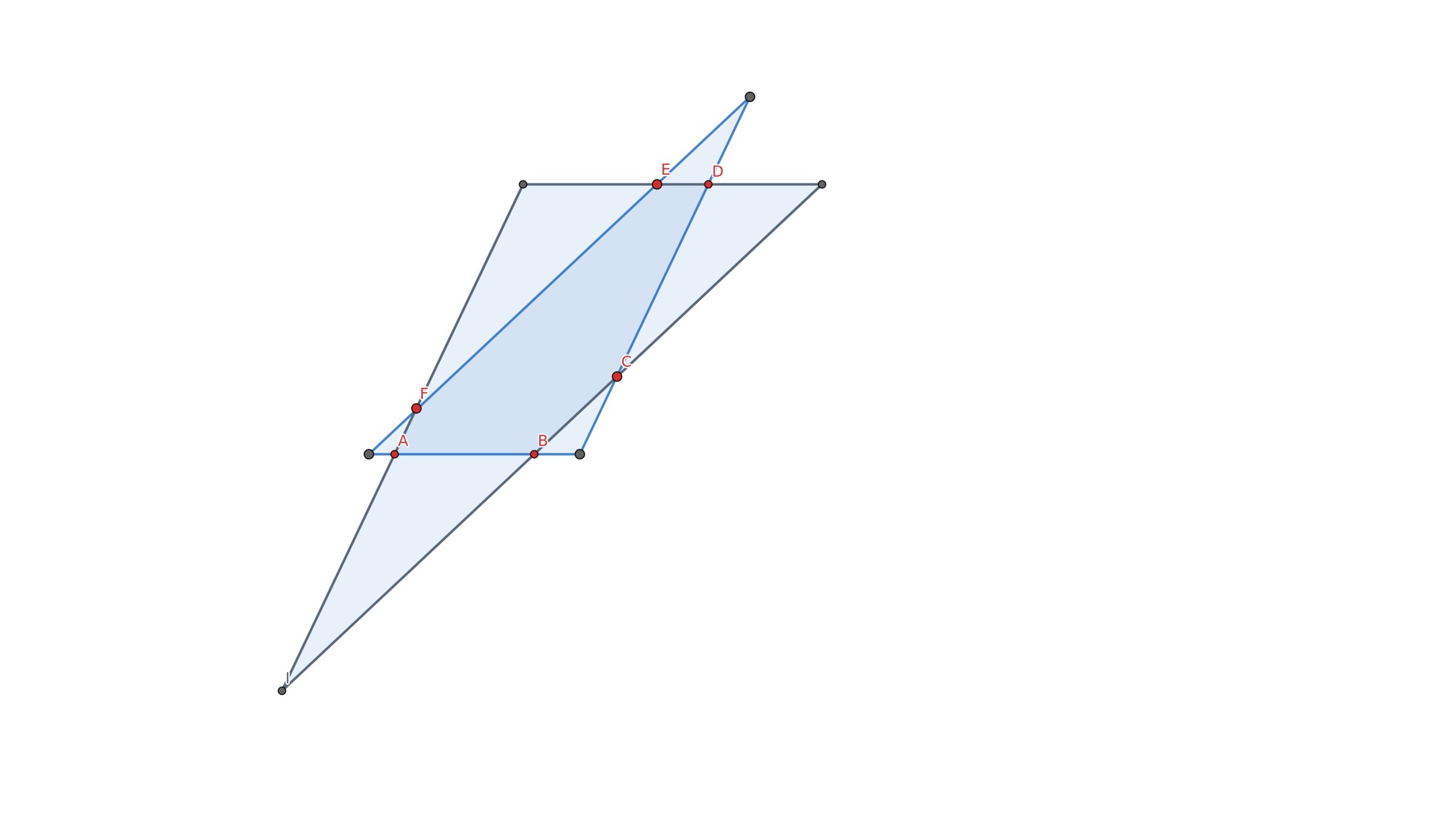
Exagon intersections
Consider two triangles T 1 and T 2 with respective sides parallel. This traingles form an irregular exagon A B C D E F . The area of this exagon is the half of the area of T 1 and is the 7 2 4 9 of T 2 . Also A B = 4 D E . Find B C ⋅ D E ⋅ F A A B ⋅ C D ⋅ E F . The result is in the form b a where a and b are positive coprime integers. Answers with a + b . The picture isn't in scale.
The answer is 103.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I decided to work with coordinates. The figure can be resized and skewed without changing the given ratios, so I decided to go with A = ( 0 , 0 ) and D = ( 1 0 , 1 0 ) . The other points I named and for simplicity, I'll give them the same names as @David Vreken
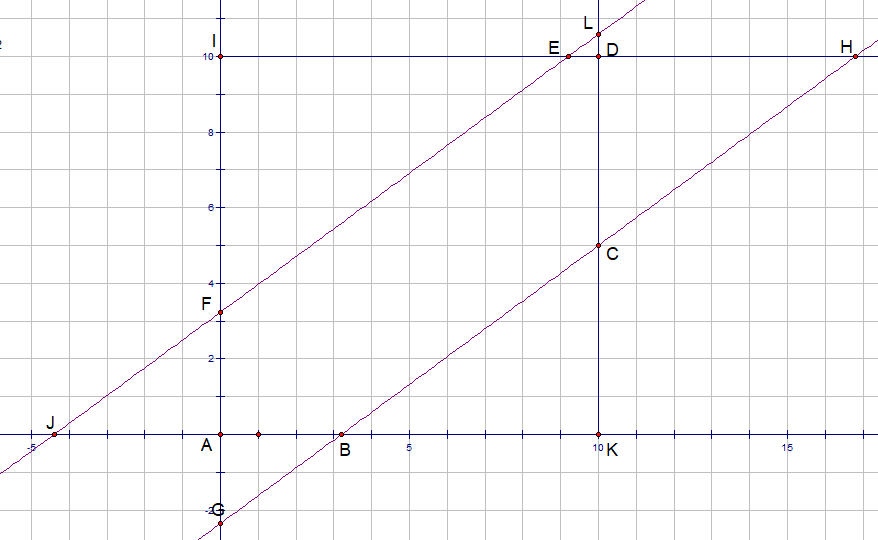
The line through I called J , F , E , L y = m x + b and gave G coordinates ( 0 , − c ) .
Now we can find the coordinates of other points in terms of b , m , c : B = ( m c , 0 ) , C = ( 1 0 , 1 0 m − c ) , E = ( m 1 0 − b , 1 0 ) , F = ( 0 , b ) , H = ( m 1 0 + c , 1 0 ) , I = ( 0 , 1 0 ) , J = ( m − b , 0 ) , K = ( 1 0 , 0 ) , L = ( 1 0 m + b , 1 0 ) ..
The triangle areas work out to T 1 = 2 m ( 1 0 + c ) 2 and T 2 = 2 m ( 1 0 m + b ) 2
We are given that 2 1 T 1 = 7 2 4 9 T 2 , from which we can solve to find c = 6 7 ( 1 0 m + b ) − 1 0 .
We are also given 4 ⋅ D E = A B , or 4 ⋅ ( 1 0 − m 1 0 − b ) = m c from wich we can solve to find m = 1 7 0 1 8 0 − 1 7 b and c = 1 7 4 0 .
So now we can give the triangles in terms of b alone: 2 1 T 1 = 1 7 ( 1 8 0 − 1 7 b ) 1 1 0 2 5 0
as well as the area of the exagon, which after much simplifying becomes: 1 7 ( 1 8 0 − 1 7 b ) 6 3 5 0 0 + 2 3 8 0 0 b − 2 8 9 0 b 2
equating these areas gives a quadratic in b whose two solutions are b = 5 and b = 1 7 5 5
I've run out of time... both values of b end up giving different looking figures but the same final ratio: 1 1 9 2 so a + b = 9 2 + 1 1 = 1 0 3
Since respective sides of T 1 and T 2 are parallel, all triangles in the diagram have congruent alternate interior, corresponding, or vertical angles; so they are all similar. Let D E = a , D L = b , and E L = c . Since A B = 4 D E , let corresponding sides of △ A B G be 4 times bigger than the sides of △ D E L . Also let △ A J F be p times bigger than △ D E L , △ K B C be q times bigger than △ D E L , △ D H C be r times bigger than △ D E L , and △ I E F be s times bigger than △ D E L .
Let θ be the angle between a and b , let b = n a , and k = 2 1 n sin θ . Then the area of a triangle with sides m a , m b , and m c is A = 2 1 ⋅ m a ⋅ m b ⋅ sin θ = 2 1 ⋅ m a ⋅ m ⋅ n a ⋅ sin θ = 2 1 n m 2 a 2 sin θ = k m 2 a 2 . Therefore, the area of △ G H I is T 1 = k ( s + r + 1 ) 2 a 2 and the area of △ J K L is T 2 = k ( p + q + 4 ) 2 a 2 . Also, the area of △ E F I is A E F I = k s 2 a 2 , the area of △ C D H is A C D H = k r 2 a 2 , and the area of △ A B G is A A B G = 1 6 k a 2 .
Let M be the area of the exagon. We are given that M = 2 1 T 1 = 2 1 k ( s + r + 1 ) 2 a 2 and M = 7 2 4 9 T 2 = 7 2 4 9 k ( p + q + 4 ) 2 a 2 . Equating these and simplifying gives us 6 ( s + r + 1 ) = 7 ( p + q + 4 ) .
Since △ G H I ∼ △ L E D , we have the proportion a s a + a + r a = b s b + p b + 4 b = c r c + q c + 4 c . From these we can deduce that p = r − 3 and q = s − 3 , and substituting these into 6 ( s + r + 1 ) = 7 ( p + q + 4 ) gives us r + s = 2 0 .
We also know that T 1 = M + A E F I + A C D H + A A B G . Substituting known expressions gives us k ( s + r + 1 ) 2 a 2 = 2 1 k ( s + r + 1 ) 2 a 2 + k s 2 a 2 + k r 2 a 2 + 1 6 k a 2 , which simplifies to ( s + r + 1 ) 2 = 2 ( s 2 + r 2 + 1 6 ) .
This equation and r + s = 2 0 solves to r = 2 1 7 and s = 2 2 3 , which means p = 2 1 1 and q = 2 1 7 .
Therefore, B C ⋅ D E ⋅ F A A B ⋅ C D ⋅ E F = q c ⋅ a ⋅ p b 4 a ⋅ r b ⋅ s c = q p 4 r s = 2 1 7 ⋅ 2 1 1 4 ⋅ 2 1 7 ⋅ 2 2 3 = 1 1 9 2 , and 9 2 + 1 1 = 1 0 3 .