Examining the slide
 Imagine that the we are examining bacteria on a slide under a microscope. The slide is represented as a two-dimensional grid of cells, each of which is either empty or filled. If the cell is empty we associate it with
and if the cell is filled we associate it with
. Any group of cells which are connected horizontally,vertically or diagonally is called a
blob
. We want to write a program to estimate the severity of infection.
Imagine that the we are examining bacteria on a slide under a microscope. The slide is represented as a two-dimensional grid of cells, each of which is either empty or filled. If the cell is empty we associate it with
and if the cell is filled we associate it with
. Any group of cells which are connected horizontally,vertically or diagonally is called a
blob
. We want to write a program to estimate the severity of infection.
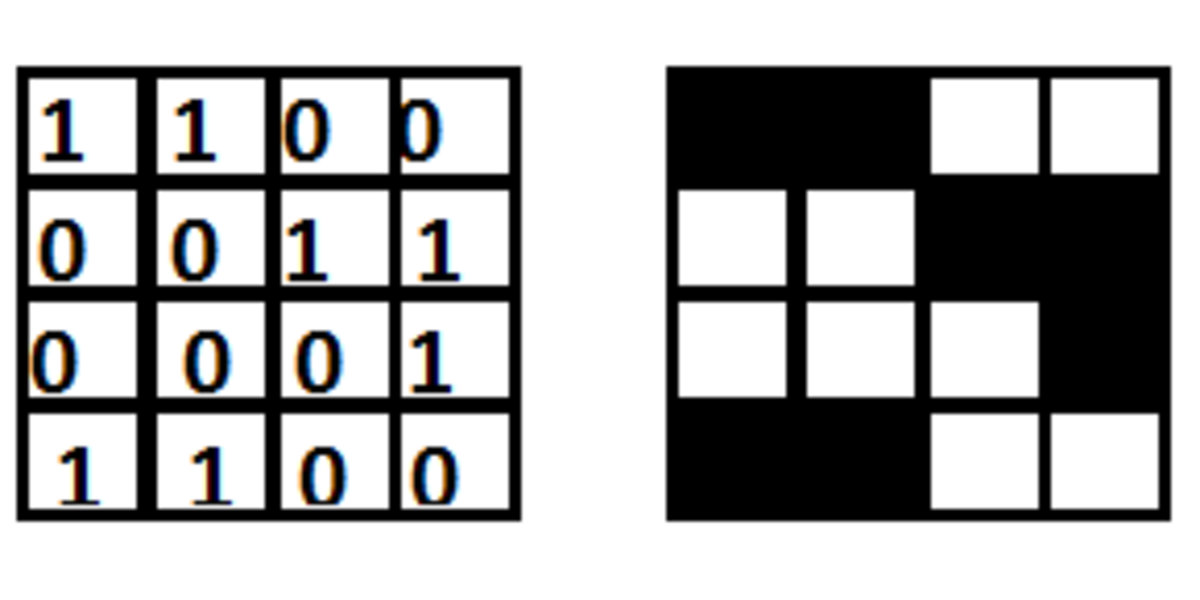
For example, there are blobs in the example above, the largest of which constitutes of cells. What is the size of the largest blob in in this square matrix ?
The answer is 122.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider every black cell as a vertex of a graph. For each one, look around and create an edge for each neighbour black cell.
The problem is now to compute the size of each connected part of the graph. This can be done by assigning value 1 to each black cell and remove them one after another: e.g. if A is connected to B, C and D:
When a vertex has no more edges, its value gives the size of its connected part.