Excircle Tangency Points

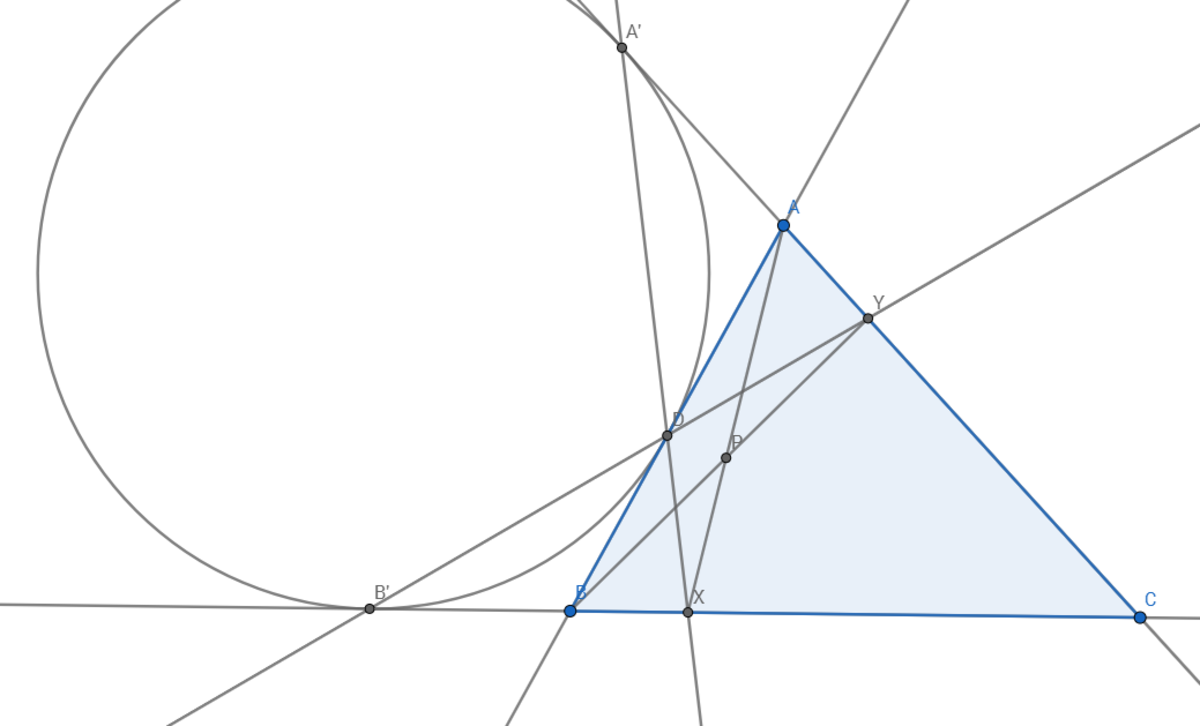
(Geogebra couldn't let me input $A'$ and $B',$ so I replaced them with A1 and B1 in the diagram.)

This is going to be a very long solution. If you have a shorter solution than this, then please post it!

For simplicity, let $A = \angle BAC, B = \angle ABC.$ Also, we will let $BC = a, CA = b, AB = c,$ and $s = \frac{a + b + c}{2}.$

First, we'll prove this lemma:

Lemma 1: $\dfrac{A'B'}{AB} = 2 \cos \dfrac{A}{2} \cos \dfrac{B}{2}.$

Consider a general acute triangle $ABC,$ and let the $C$ -excircle with center $E$ be tangent at $A', B', D$ as shown in the diagram.

Let $I$ be the incenter of $\triangle ABC.$ Note that

$\angle B'A'D = \dfrac{1}{2} \angle B'ED = \dfrac{1}{2} (180 - \angle DBB') = \dfrac{B}{2} = \angle IBA.$

Similarly, $\angle A'BD = \dfrac{A}{2} = \angle IAB.$ Therefore, $\triangle A'B'D \sim \triangle BAI.$

We can find that $A'D = 2(s - a) \cos \frac{A}{2}$ and $BI = \frac{s - a}{\cos \frac{B}{2}},$ so

$\dfrac{A'B'}{AB} = \dfrac{A'D}{BI} = \dfrac{2(s - a) \cos \frac{A}{2}}{\frac{s - a}{\cos \frac{B}{2}}} = 2 \cos \dfrac{A}{2} \cos \dfrac{B}{2}. \, \blacksquare$

Next, we will find $\frac{BX}{XC}$ and $\frac{AY}{YC}.$ To accomplish this, we will find the lengths of $B'X, XC, A'Y, YC$ via the Ratio Lemma, then use the facts that $BX = B'X - B'B$ and $AY = A'Y - A'A.$

Before moving on, we note that $\angle CA'X = \frac{A}{2}$ and $\angle CB'Y = \frac{B}{2}.$

Lemma 2: $\dfrac{B'X}{XC} = \dfrac{-a + b + c}{a}, \dfrac{A'Y}{YC} = \dfrac{a - b + c}{b}$

By the results of Lemma 1, we have $A'B' = 2c\cos \frac{A}{2} \cos \frac{B}{2}.$ Now, applying the Ratio Lemma for $\frac{B'X}{XC}$ in $\triangle A'B'C,$ we have

$\begin{aligned} \dfrac{B'X}{XC} &= \dfrac{A'B'}{A'C} \cdot \dfrac{\sin \angle B'A'X}{\sin \angle CA'X} \\ &= \dfrac{2c\cos \frac{A}{2} \cos \frac{B}{2}}{s} \cdot \dfrac{\sin \frac{B}{2}}{\sin \frac{A}{2}} \\ &= \dfrac{c\cos \frac{A}{2} \sin B}{s\sin \frac{A}{2}}. \end{aligned}$

We know that $\cos \frac{A}{2} = \sqrt{\frac{s(s - a)}{bc}}$ and $\sin \frac{A}{2} = \sqrt{\frac{(s - b)(s - c)}{bc}}$ :

$\begin{aligned} \dfrac{c\cos \frac{A}{2} \sin B}{s\sin \frac{A}{2}} &= \dfrac{c \sin B}{s} \sqrt{\dfrac{s(s - a)}{(s - b)(s - c)}} \\ &= \dfrac{c(s - a) \sin B}{\sqrt{s(s - a)(s - b)(s - c)}}. \end{aligned}$

We recognize the denominator as $[ABC],$ by Heron's formula. By another area formula, we also have $\sin B = \frac{2 [ABC]}{ac}.$ Thus,

$\begin{aligned} \dfrac{B'X}{XC} &= \dfrac{c(s - a) \sin B}{\sqrt{s(s - a)(s - b)(s - c)}} \\ &= \dfrac{c(s - a) \frac{2 [ABC]}{ac}}{[ABC]} \\ &= \dfrac{2(s - a)}{a} \\ &= \dfrac{-a + b + c}{a}. \end{aligned}$

Using the same strategy, we can find $\frac{A'Y}{YC} = \frac{a - b + c}{b}. \, \blacksquare$

Now, we can find $\frac{BX}{XC}$ and $\frac{AY}{YC}$ :

Lemma 3: $\dfrac{BX}{XC} = \dfrac{s-a}{s}, \dfrac{AY}{YC} = \dfrac{s-b}{s}$

Again, we'll focus solely on the points and segments on ray $CB.$ By Lemma 2, $B'X = \frac{-a + b + c}{a}XC.$ We also have $B'X + XC = s,$ by the properties of the excircle. Thus,

$\begin{aligned} B'X + XC &= s \\ XC \left ( \dfrac{-a + b + c}{a} + 1 \right ) &= s \\ XC \left ( \dfrac{b + c}{a} \right ) &= s \\ XC &= \dfrac{sa}{b + c}. \\ B'X &= s - \dfrac{sa}{b + c}. \end{aligned}$

Next, we apply $BX = B'X - B'B$ :

$\begin{aligned} BX &= B'X - B'B \\ &= s - \dfrac{sa}{b + c} - (s - a) \\ &= a - \dfrac{sa}{b + c} \\ &= a \left ( 1 - \dfrac{a + b + c}{2(b + c)} \right ) \\ &= \dfrac{a(-a + b + c)}{2(b + c)} \\ &= \dfrac{a(s - a)}{b + c}. \end{aligned}$

Finally,

$\dfrac{BX}{XC} = \dfrac{\frac{a(s - a)}{b + c}}{\frac{sa}{b + c}} = \dfrac{s - a}{s}.$

In a similar vein, we can find that $\frac{AY}{YC} = \frac{s-b}{s}. \, \blacksquare$

Here's the last observation before we can calculate our final answer:

Lemma 4: $C, P, D$ are collinear.

Suppose $CP$ intersects $AB$ at point $Z.$ By Ceva's Theorem, $\frac{ZB}{ZA} \cdot \frac{XB}{XC} \cdot \frac{YC}{YA} = 1.$ Applying the results of Lemma 3 yields

$\begin{aligned} \frac{ZB}{ZA} \cdot \frac{XB}{XC} \cdot \frac{YC}{YA} &= 1 \\ \dfrac{ZB}{ZA} \cdot \frac{s - a}{s} \cdot \dfrac{s}{s - b} &= 1 \\ \dfrac{ZB}{ZA} &= \dfrac{s - b}{s - a}. \end{aligned}$

However, $\frac{DB}{DA} = \frac{s - b}{s - a}$ as well. Since there only exists one point along line $AB$ with this ratio, we conclude $Z = D,$ and $D$ lies on $CP. \, \blacksquare$

We can finally find $\frac{CP}{PD}$ , using Lemma 3, Lemma 4, and van Aubel's Theorem:

$\begin{aligned} \dfrac{CP}{PD} &= \dfrac{CX}{XB} + \dfrac{CY}{YA} \\ &= \dfrac{s}{s - a} + \dfrac{s}{s - b} \\ &= \dfrac{21}{21 - 13} + \dfrac{21}{21 - 14} \\ &= \dfrac{21}{8} + 3 \\ &= \dfrac{45}{8}. \end{aligned}$

Our final answer is $p + q = 45 + 8 = \boxed{53}.$