Exciting Sequences

I just noticed my old solution was invalid.

Here is the alternative valid solution,

There are obviously the same number of terms in the top and bottom, since for each term $k$ in the top,a $k+1$ corresponds in the bottom. The ratio is equal to

$\frac{ \frac{terms_{top}}{2} (T_{1st}+T_{last)} }{ \frac{terms_{bottom}}{2} (B_{1st}+B_{last})}$

,but since the numbers of terms are the same, the first terms cancel and we are left with

$\frac{T_{1st} + T_{last}}{B_{1st} + B_{last}} = \frac{1+199}{2+200} = \frac{200}{202} = \boxed{\frac{100}{101}}$

(1+199)+(3+197)+......+(97+103)+(99+101) / (2+200)+(4+198)+.....+(98+104)+(100+102)= (50)(200)/(50)(202)=100/101

The ratio can be written as

$\frac {\displaystyle \sum_{i=0}^{99}(2 \cdot i+1)}{\displaystyle \sum_{i=0}^{99}(2 \cdot i+2)} = \frac {\displaystyle 100 + \sum_{i=0}^{99}(2 \cdot i)}{\displaystyle 200 + \sum_{i=0}^{99}(2 \cdot i)} = \frac {\displaystyle 100 + 2 \cdot \sum_{i=0}^{99}i}{\displaystyle 200 + 2 \cdot \sum_{i=0}^{99}i}$

The summation 1+2+...+99 is equal to 0+99+1+98+...+49+50 which is equal to $50 \cdot 99$ . Think of it like folding the two sides of summation in order to create the same number in each addition. There is a famous anecdote from Gauss' life on this arithmetic progression. Finally:

$\frac {\displaystyle 100 + 2 \cdot 50 \cdot 99}{\displaystyle 200 + 2 \cdot 50 \cdot 99} = \frac {\displaystyle 100 + 100 \cdot 99}{\displaystyle 100 \cdot 2 + 100 \cdot 99} =$

If you divide both numerator and denominator with 100 then:

$= \frac {\displaystyle 1 + 1 \cdot 99}{\displaystyle 2 \cdot 1 + 1 \cdot 99} = \frac {\displaystyle 100}{\displaystyle 101}$

Using two very familiar summation formulae:

The sum of odd integers $1 ... 2n - 1$ is $n^2$

The sum of integers 1,2,...,n is $\frac { n(n+1)}{2}$

The given expression can be written as $\frac{n^2}{ 2( \frac { n(n+1)}{2})}$ $= \frac {n} {n+1}$ with n = 100.

Therefore the answer is $\boxed { \frac{100}{101}}$

• $\frac{1+3+5+...+199}{2+4+6+...+200}$ Adding 1 in each term in Numerator and Subtracting 100 We get $\frac{2+4+6+...200 - 100}{2+4+6+...200}$ = 1 - $\frac{100}{2.50.101}$ = 1 - $\frac{1}{101}$ = $\frac{100}{101}$

~1+3+5+...+199=100*100=10000 (Sum of The first n odd numbers)

~2+4+6+...+200=(200 201)/2-100 100=10100 ((I used The fact that The Sum of The first n numbers is given by n(n+1)/2 and The Sum of The first n odd numbers is n*n; subtracting this two numbers we Will find The Sum of The first n Even numbers.(There is also The Way to find this number using The formula of The Sum of The first n Even number But I didn't remember it ahahah))

So The results is 10000/10100=100/101.

Sorry for My English ahaha

$\frac{\sum_{k=1}^{100} (2k -1)}{\sum_{\ell=1}^{100} 2\ell} =\frac{\sum_{k=1}^{100} 2k \ - 100}{\sum_{\ell=1}^{100} 2\ell} =1 -\frac{100}{2\sum_{\ell=1}^{100}\ell} = 1 - \frac{100}{100\cdot101} = 1 - \frac{1}{101} = \frac{100}{101}.$

½ no of odd nos x sum of first and last odd number ÷ ½ no of even nos + sum of first and last even no

hint: use gausses method for summing numbers

btw I love how old these problems are like there are some 8 years old comments in here

We can express both numenator and denominator with a sum:

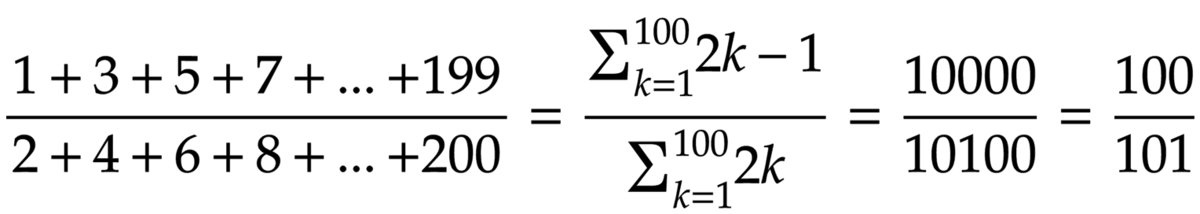
The solution is $\frac{100}{101}$ .

First, let's deduce the sum of the numerator, 1+3+5+7+...+199 (which is really the sum of all the odd numbers from 1 till 200).

*1 can "pair up" with 199 to give 200. The same goes for 3 and 197, 5 +195, etc... until 99+101.
*Since there are 50 odd numbers in the first 100 integers, and 50 more in the next 100 integers, we can sum exactly 50 pairs in this manner. This implies:

Numerator = 50(200) = 10 000

The same process can be applied to the denominator, except for the pair 100+200 that yields 300 instead of 200. That is 100 more than the other pairs, so:

Denominator = 50(200)+100 = 10 100

Hence, $\frac{10 000}{10 100}$ = $\frac{100}{101}$

First find the value of 'n' (no of terms) in both numerator and denominator . Then use the formula→ Sn= n÷2(a+l) in both numerator and denominator u will get '6700' in NUMERATOR and '6767' in DENOMINATOR. by simplifing u will get 100÷101

= $\frac{1 + 3 + 5 + ... + 199}{2 + 4 + 6 + ... +200}$ = $\frac{100 \times 100 }{100 \times 101}$ = $\frac{100}{101}$

Apply the concept of Arithmetic Progression..... For instant answer....."hmm"...trust me..

First write the equation as: $\frac{x - 100}{x} = y$

$y = 1 - \frac{100}{x}$

Use arithmetic series equation:

$x = \frac{n(a_1 + a_n)}{2} = \frac{100(2 + 200)}{2} = 50(202)$

$y = 1 - \frac{100}{50 ( 202 )} = 1 - \frac{1}{101} = \frac{100}{101}$

(N^2) / N(N+1), here N=100, so 10000 / 10100 = 100/101

1+3+...+199=100^2, 2+4+...+200=2(1+2+...+100)=100 101 hence 100^2/(100 101)=100/101

$There\quad are\quad 100\quad pairs,\quad Those\quad sum\quad is\quad 200\quad (Ex,(1+199),(3+197),......(99+101)\quad etc.)\quad on\quad the\quad Numerator.\\ And\quad 100\quad pairs,\quad Those\quad sum\quad is\quad 202\quad (Ex,(2+200),(4+198),......(100+102)\quad etc.)\quad on\quad the\quad Denominator.\\ So,\quad \frac { 1+3+5+......+199 }{ 2+4+6+......+200 } =\frac { 100\times 200 }{ 100\times 202 } =\frac { 200 }{ 202 } =\boxed { \frac { 100 }{ 101 } }$

Express a/b as ((a+b) - b)/b where a is the sequence 1+3+...199 and b is the sequence 2+4+...200

This becomes ((1...200) -(1..100))/(1 ... 100) which simplifies to ((200 X 201) - (100 X 101))/(100 X 101) using the summation of series and removing division by 2 from each expression leaving (201-101)/101 = 100/101