This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
x+y+z=6
2x+y+z=x+x+y+z=7
x+6=7
x=1
and y =2 and z=3
then xyz=6
in each case the sum is increasing by one value. in the first step,when x is doubled the value is only increasing by one. in next step if y is doubled,the value is increasing by one more value. therefore,x<y<z. therefore,least possible values are : (x,y,z)=(1,2,3) hence,(xyz)=1 2 3 =6.
ya
Since x + y + z = 6
then
2 x + y + z = x + ( x + y + z ) = x + 6 = 7 yields x = 1
Since x = 1 , we can make the second equation and third equation in the form:
y + z = 5 and 2 y + z = 7
By elimination, y = 2 and z = 3 .
Thus, x y z = 1 × 2 × 3 = 6
if assume, X=1,Y=2,Z=3
which satisfies the above given equations.
Hence we can say,,xyz =6. i
taking any two equations and try to reduce three variables to two and then solve the equations to get the value of those two variable to get the third variable value.
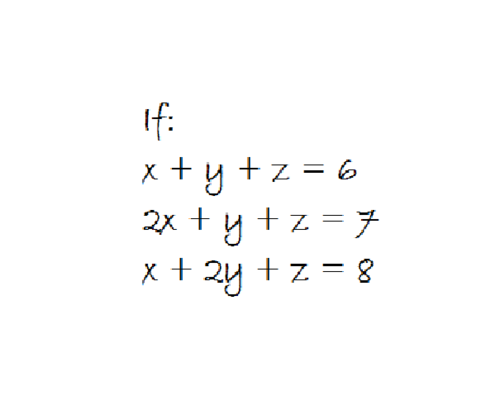
by solving any of the 2 equations, we get x=1. by substituting th value of x and solving another 2 equations, we get y=2. substitute x and y values in any of the equations,we get z=3. by multiplying, we get xyz=6