Extraordinary Ellipse
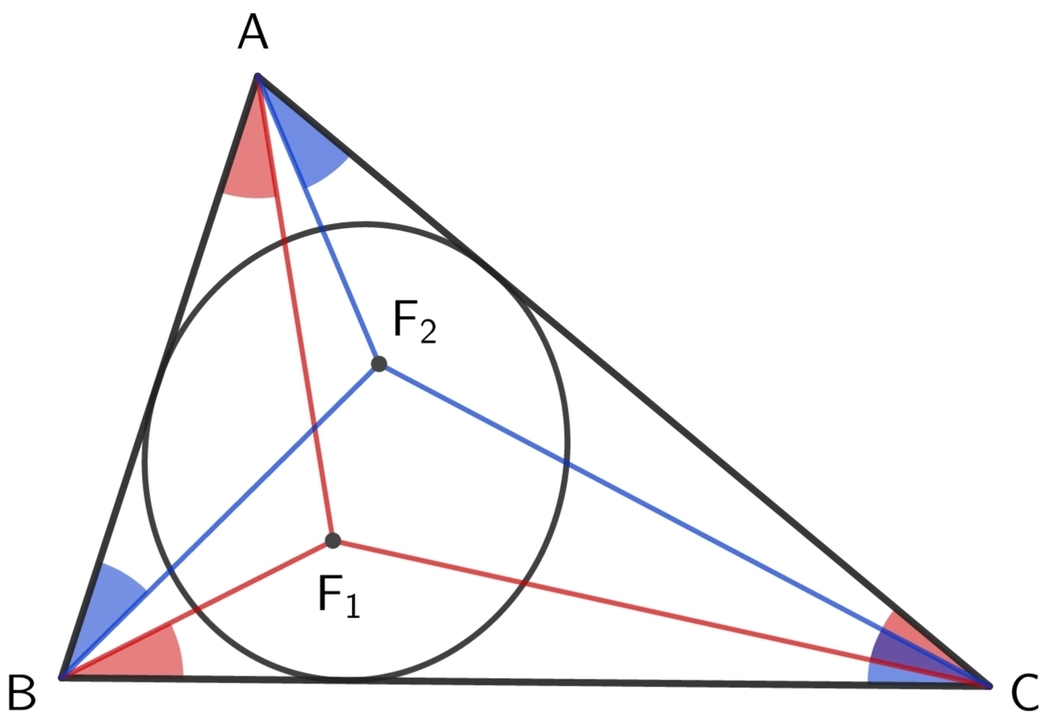 An ellipse is inscribed in a triangle of angles
7
π
,
7
2
π
, and
7
4
π
.
An ellipse is inscribed in a triangle of angles
7
π
,
7
2
π
, and
7
4
π
.
The foci F 1 and F 2 of the ellipse are such that
{ ∠ F 1 A B = ∠ F 1 B C = ∠ F 1 C A ∠ F 2 A C = ∠ F 2 B A = ∠ F 2 C B
Find the eccentricity of the ellipse.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We are looking at the Brocard inellipse of the triangle, which has foci at the first and second Brocard points. and semimajor and semiminor axes A = 2 a 2 b 2 + b 2 c 2 + c 2 a 2 a b c B = a 2 b 2 + b 2 c 2 + c 2 a 2 2 a b c Δ and hence eccentricity E = 1 − A 2 B 2 = a 2 b 2 + b 2 c 2 + c 2 a 2 a 4 + b 4 + c 4 − 1 where a , b , c are the sides of the triangle. Putting a = sin 7 π , b = sin 7 2 π and c = sin 7 4 π into this formula gives E = 2 1 .
Here is a detailed, but elementary, proof of the above.
First note the following triangle identities: cot A cot B cot C + csc A csc B csc C cot A cot B + cot A cot C + cot B cot C = cot A + cot B + cot C = 1 The first follows because 2 cos 2 ( 2 1 ( u + v + w ) ) ≡ sin u sin v sin w [ cot u cot v cot w − cot u − cot v − cot w + csc u csc v csc w ] for any u , v , w , and hence the fact that A + B + C = π gives the result. The second follows because cot C = cot ( π − A − B ) = cot A + cot B 1 − cot A cot B Applying the Sine Rule to the triangles A B P . B P C and C P A , we see that sin ( B − ω ) y a = sin ω y b sin ( C − ω ) y b = sin ω y c sin ( A − ω ) y c = sin ω y a and hence sin ( A − ω ) sin ( B − ω ) sin ( C − ω ) ( cot ω − cot A ) ( cot ω − cot B ) ( cot ω − cot C ) cot 3 ω − ( cot A + cot B + cot C ) cot 2 ω + cot ω − ( cot A + cot B + cot C ) ( cot ω − cot A − cot B − cot C ) ( ω 2 + 1 ) = sin 3 ω = csc A csc B csc C = 0 = 0 and hence the Brocard angle ω is unique, and cot ω = cot A + cot B + cot C More applications of the Sine Rule tell us that sin ω y a = sin A b sin ω y b = sin B c sin ω y c = sin C a and hence y a = a 2 R b sin ω y b = b 2 R c sin ω y c = c 2 R a sin ω where R is the circumradius of A B C . If we drop perpendiculars from P to the sides B C , C A , A B , with feet D , E , F and lengths x a , x b , x c respectively, simple trigonometry tells us that x a = y b sin ω = b 2 R c sin 2 ω x b = y c sin ω = c 2 R a sin 2 ω x c = y a sin ω = a 2 R b sin 2 ω Of course, x a : x b : x c are the absolute triangular coordinates of the point P .
We note that P Q 2 = ( c − y a cos ω − p b cos ω ) 2 + ( x c − q c ) 2 so that 4 R 2 P Q 2 = ( sin C − ( b a + a b ) sin ω cos ω ) 2 + ( b a − a b ) 2 sin 4 ω = sin 2 ω ( 1 − 4 sin 2 ω ) after much simplification. Thus P Q = 2 R sin ω 1 − 4 sin 2 ω .
For any point X on B C , note that P X + Q X = P ′ X + Q X , where P ′ is the mirror image of P in B C . It is clear that P X + Q X ≥ P ′ Q , and that this least value is achieved when X = X 0 . Now P ′ Q 2 = ( c − y a cos ω − p b cos ω ) 2 + ( x c + q c ) 2 so that 4 R 2 P ′ Q 2 = ( sin C − ( b a + a b ) sin ω cos ω ) 2 + ( b a + a b ) 2 sin 4 ω = sin 2 ω Thus P ′ Q = 2 R sin ω .
For this particular problem, cot ω = cot 7 π + cot 7 2 π + cot 7 4 π = 7 so that sin ω = 2 2 1 , and hence E = 1 − 4 sin 2 ω = 2 1 .