Exoplanet transit I

Classical Mechanics Level 3

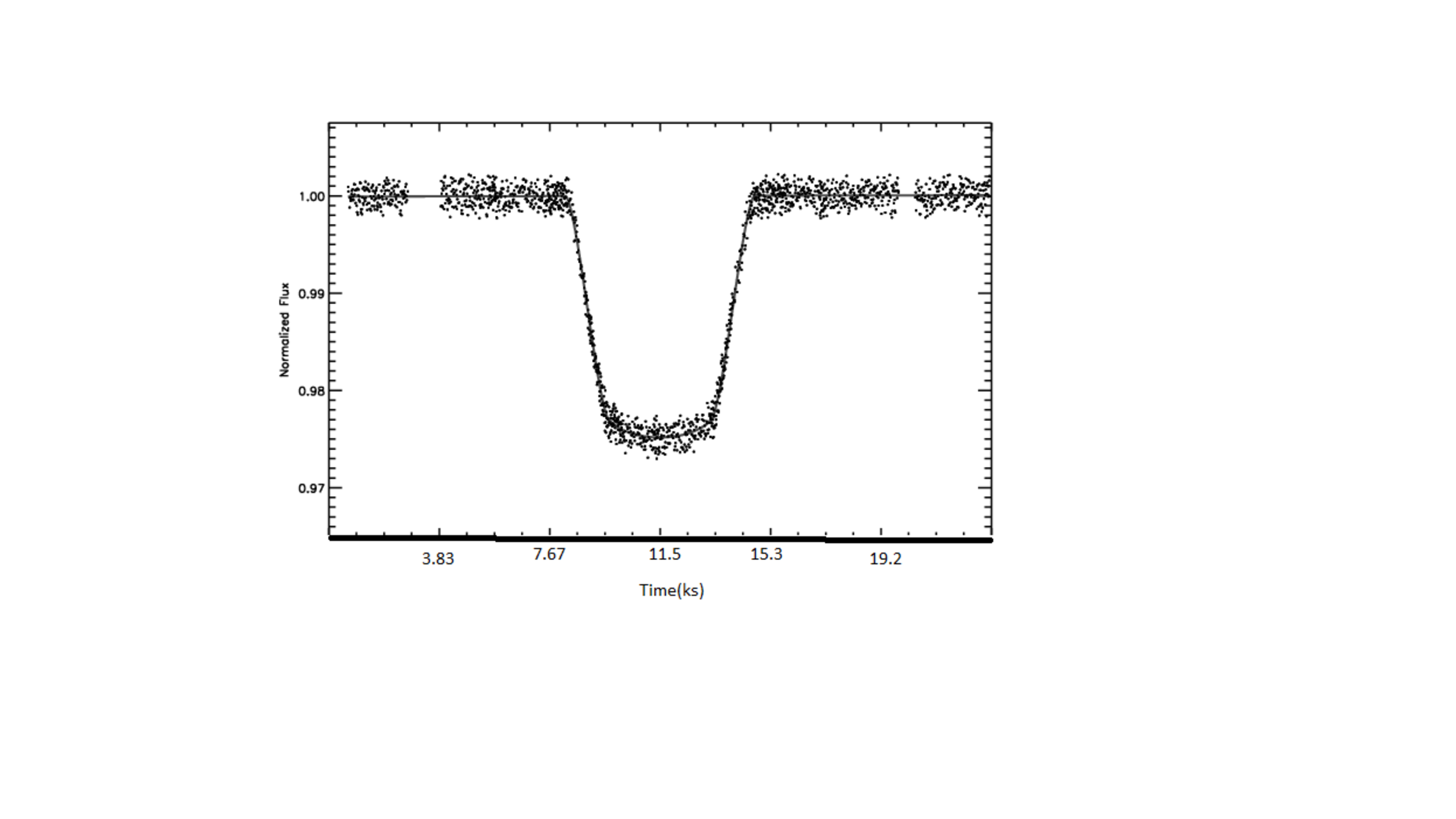
This figure shows the light curve caused by the transit of the exoplanet HD189733b, which orbits an star with 0.8M☉(solar mass). The vertical axis shows the normalized flux of the host star and the horizontal axis shows the time.

What is the ratio r R \frac{r}{R} between the radius of the exoplanet( r ) and the radius of the star( R ) ? Assumptions and details

  • M☉ = 2 × 1 0 30 2\times 10^{ 30 } kg

  • The orbital period of the planet is 2.218573 days.

Hint - You will have to use the graph

0.987 1.58E-2 0.158 9.87E-2

Fabrizio Melges Ferro by Fabrizio Melges Ferro , 17, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The amount of light that is blocked [ B ] (which can be determined by the graph) is about 1 - 0.975 = 0.025 ;This amount equals the area of the disk of the exoplanet divided by the area of the disk of the star

B= π r 2 π R 2 \frac{\pi { r }^{ 2 }}{\pi { R }^{ 2 }}

0.025= r 2 R 2 \frac { { r }^{ 2 } }{ { R }^{ 2 } }

0.025 = r R \sqrt { 0.025\quad } =\quad \frac { r }{ R }

0.158 = r R 0.158\quad =\quad \frac { r }{ R }

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...