Expanding Triangle
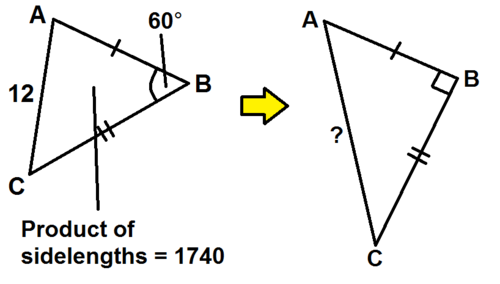 When
∠
ABC = 60°, AC = 12 and the product of the sidelengths of Triangle ABC is 1740.
When
∠
ABC = 60°, AC = 12 and the product of the sidelengths of Triangle ABC is 1740.
What is the new length of AC if ∠ ABC is increased to 90° and AB and BC are kept constant length?
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The length we want to find can be written as a 2 + c 2 as it is a right angled triangle. Now the cosine rule states that b 2 = a 2 + c 2 − 2 a c cos B therefore by rearranging we have an expression describing the first triangle b 2 + 2 a c cos B = a 2 + c 2 So by simply plugging in the values for b and B we have the unknown quantity a c . The product of the side lengths of the first triangle is 1 7 4 0 therefore by dividing by 1 2 we get 1 4 5 = a c finishing the formula plugging in we get our answer to be 1 7 .
∠ABC = 60°, AC = 12 and AB*BC = 145, are you sure such a triangle can exist
First of all, we see that ( A B ) B C = 1 2 1 7 4 0 = 1 4 5 . Using Law of Cosines in the first △ A B C , we get that A C 2 = A B 2 + B C 2 − 2 ( A B ⋅ B C ) ( c o s 6 0 ) = A B 2 + B C 2 − 2 9 0 ( 0 . 5 ) = A B 2 + B C 2 − 1 4 5 So, 1 2 2 = A B 2 + B C 2 − 1 4 5 Then, 2 8 9 = A B 2 + B C 2 We use that in the new △ A B C , and we get that A C 2 = 2 8 9 = A B 2 + B C 2 So, A C = 1 7